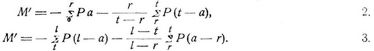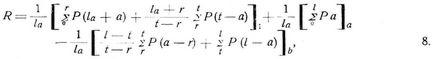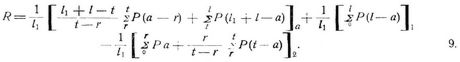Gelenkträger, durchlaufender

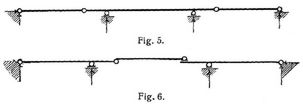
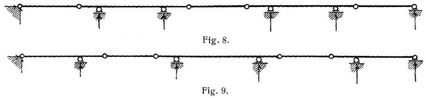
Gelenkträger, durchlaufender (Gerberscher Träger, Kragträger). Während die Stützenreaktionen eines Balkenträgers (s. Balken, Bd. 1, S. 503) auf zwei Stützen mit frei drehbaren Enden (Fig. 1) aus Beziehungen der reinen Statik bestimmt werden können (s. Balken, einfache, Bd. 1, S. 519), fehlen bei mehr als zwei Stützen (Fig. 2) zur statischen Bestimmtheit der Stützenreaktionen ebensoviel Gleichungen, als Zwischenstützen vorhanden sind (s. Balken, durchlaufende, Bd. 1, S. 507). Hierdurch wird nicht nur die Berechnung umständlicher und weniger zuverlässig, sondern es erlangen auch unbeabsichtigte Höhenänderungen der Stützpunkte und gewisse Temperaturänderungen Einfluß auf die Beanspruchungen (Bd. 1, S. 512, 513). Um aus solchen durchlaufenden Trägern eine statisch bestimmte Trägerart (s. Träger) herzustellen, hat man bei n Zwischenstützen n Zwischengelenke eingeschaltet, womit der durchlaufende (kontinuierliche) Gelenkträger entstanden ist. Da das Moment der äußeren Kräfte, (s.d.) auf einer Seite jedes Gelenks gleich Null sein muß, weil die Resultante dieser Kräfte[362] bei der üblichen Vernachlässigung der Reibung durch den Gelenkmittelpunkt geht (vgl. Gelenke), so erhalten wir eine der Anzahl der Zwischenstützen entsprechende Anzahl neuer Gleichungen, wonach alle Stützenreaktionen ohne außerstatische Hilfsmittel (Elastizitätslehre) bestimmt werden können. Vorausgesetzt ist hierbei, daß die Gelenke in geeigneter Weise auf die einzelnen Oeffnungen verteilt werden (s. Träger); Fig. 3–9 zeigen richtige Anordnungen von zwei bis fünf Oeffnungen. Doch kann das bei einer Endstütze angedeutete, horizontal frei verschiebbare Gelenkauflager (vgl. Auflager) stets auch innerhalb einer Oeffnung angeordnet werden, so daß z.B. bei drei Oeffnungen neben den Anordnungen Fig. 4 und 5 auch die Anordnung Fig. 6 mit statischer Bestimmtheit und Stabilität der Trägerart verträglich ist.

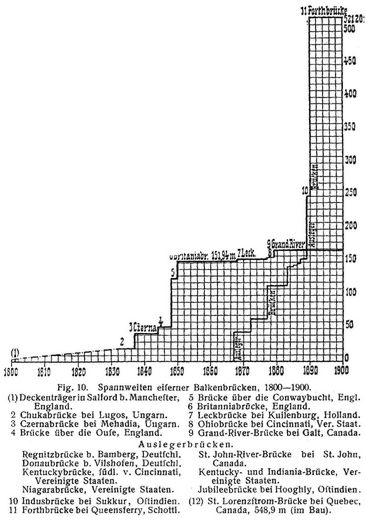
Obwohl es Balkenanordnungen, welche man jetzt mit durchlaufenden Gelenkträgern in Verbindung bringen kann, wohl von jeher gegeben hat, ist doch die bewußte Einschaltung von Gelenken auf die obenangedeuteten theoretischen Erwägungen zurückzuführen. In England haben sich schon in den vierziger Jahren des vorigen Jahrhunderts Clark und Fowler [16], [17], in Deutschland anfangs der sechziger Jahre zuerst Köpcke und A. Ritter [1] mit denselben beschäftigt (vgl. Gelenke). Gerber ist selbständig wieder darauf gekommen [2] und ihm hat man die Einführung der durchlaufenden Gelenkträger in die Praxis zu verdanken. Erste Ausführungen: Straßenbrücke über die Regnitz bei Bamberg nach der Anordnung Fig. 4 mit Oeffnungen von 28,8 m, 45,1 m, 28,8 m, Obergurten horizontal, Untergurten schwach nach oben gekrümmt, vollendet im März 1867; Straßenbrücke über den Main bei Haßfurt, ebenfalls Fig. 4 entsprechend, Oeffnungen 23,9 m, 37,9 m, 23,9 m, Gurten symmetrisch zu einer Horizontalen, bei den Trägerenden und Zwischengelenken zusammentreffend, vollendet im Mai 1867; Straßenbrücke über die Donau bei Vilshofen, Anordnung nach Fig. 8, Oeffnungen 51,6 m, 51,6 m, 65,4 m, 51,6 m, 51,6 m, Parallelträger (s.d.), vollendet 1872, u.s.w. Seitdem sind durchlaufende Gelenkträger häufig zur Verwendung gekommen, für Eisenbahnbrücken erstmals bei der Luhebrücke [3] der Wittenberg-Buchholzer Bahn, Anordnung Fig. 4, Oeffnungen 13,653 m, 14,124 m, 13,653 m, Blechträger, vollendet 1873. Es folgten: Warthebrücke bei Posen [4], Anordnung Fig. 8, Oeffnungen 38 m, 36 in, 45 m, 36 m, 38 m, in der zweiten und vierten Oeffnung Parallelgurten mit anschließenden Konsolen, auf welchen Paulische Träger (s.d.) mit horizontalem Untergurt ruhen, vollendet 1875; Kentuckybrücke der Cincinnati-Southern-Bahn, Anordnung Fig. 5 mit Oeffnungen von je 114,3 m, vollendet 1877. Die Träger der Luhebrücke scheinen die kleinsten ausgeführten Gelenkträger im Brückenbau und zugleich die einzigen Blechträger geblieben zu sein, doch wurden für möglichst billige Brücken noch kleinere vollwandige Gelenkträger vorgeschlagen [9], und selbst bei Decken hat der kontinuierliche Gelenkträger Verwendung gefunden [6], [7]. Zu den bedeutendsten neueren Ausführungen durchlaufender Gelenkträger gehört die 1895 dem Verkehr übergebene Donaubrücke bei Cernawoda in Rumänien [20], nach der Anordnung Fig. 8, Oeffnungen 140 m, 140 m, 190 m, 140 m, 140 m, Form s. Bd. 2, S. 338, weitere Fälle s. [13], [27], [28]. Projekt einer Brücke über den Kanal [14].[363] Den Einfluß der Kragträgerbrücken oder Auslegerbrücken auf die Brückenspannweiten läßt die in Fig. 10 dargestellte Zunahme der Spannweiten eiserner Balkenbrücken im 19. Jahrhundert [25] erkennen (vgl. Spannweite). Während die Spannweiten gewöhnlicher Balkenbrücken nicht über diejenige der Grand-River-Brücke bei Galt hinausgingen (167,6 m), fliegen die Spannweiten der Auslegerbrücken auf mehr als das Dreifache (Forthbrücke 521,2, Lorenzstrombrücke 548,9 m), womit sie selbst die zur Bewältigung großer Spannweiten besonders geeigneten Hängebrücken überholten (Brooklynbrücke und Williamsburgbrücke über den East-River in New York 486,3 m und 487,7 m). Die größte Spannweite durchlaufender Gelenkträger und aller Brücken überhaupt wird die im Baue begriffene Brücke über den St. Lorenz-Strom bei Quebec in Amerika [29] mit 548,9 m besitzen (Fig. 11).

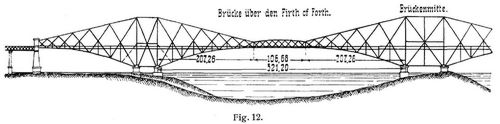
Wird bei Balken die Anzahl der Zwischengelenke geringer als die Anzahl der Zwischenstützen gewählt oder kommt ein Horizontalschub hinzu, so entsteht ein durchlaufender Gelenkträger von statisch unbestimmter Art [22], [23], [26], [30], für welchen zur Bestimmung der Stützenreaktionen die Elastizitätslehre herangezogen werden muß, wenn letztere nicht durch vereinfachende Annahmen umgangen wird. Um z.B. die Träger der Forthbrücke [12], [15], [16] mit den größten Spannweiten aller gegenwärtig vollendeten Brücken (Fig. 12, 13), deren Wirkungsweise man durch Fig. 14 zu veranschaulichen suchte, als durchlaufende Gelenkträger von statisch bestimmter Art ansehen zu können, muß das mittlere Pfeilerfeld von 79,246 m als eine Oeffnung für sich betrachtet werden, entsprechend der schon 1863 von A. Ritter gewählten Behandlung der Pfeilerfelder (Fig. 15), während die 44,195 m langen äußeren Pfeilerfelder auf die anschließenden Oeffnungen zu verteilen sind (bei vier Zwischengelenken vier Zwischenstützen). Faßt man dagegen auch die beiden äußeren Pfeilerfelder als besondere Oeffnungen auf, so tritt statische Unbestimmtheit der Trägerart ein (bei vier Zwischengelenken sechs Zwischenstützen). Um diese bei der Niagarabrücke ([8], Fig. 16) zu heben, hat man die Pfeilerfelder ohne Diagonalen hergestellt, also imaginäre Gelenke (s. Gelenkverbindung und Träger) daselbst angeordnet, womit aber eine andre Trägerart als die oben betrachtete entstanden ist.

Was die Berechnung der durchlaufenden Gelenkträger obiger Art betrifft, so ist zunächst zu beachten, daß jede Oeffnung, welche ein Zwischengelenk enthält, noch ein zweites Zwischengelenk oder ein Endgelenk aufweist (Trägerende, Fig. 3–9). Die horizontalen Entfernungen dieser Gelenke von den vorausgehenden Stützpunkten ihrer Oeffnungen seien durch r, t bezeichnet (Fig. 17). Das Trägerstück zwischen beiden Gelenken wirkt ganz wie ein einfacher Balkenträger[364] der Spannweite t – r, es ist als vollwandiger Träger nach den Formeln unter Balken, einfache, Biegung, Blechträger, als Fachwerk einfachen Systems mit Vertikalen (Ständerfachwerk) nach den unter Balkenfachwerke und eventuell nach den unter Parallelträger, Parabelträger, Paulischer Träger, Schwedler-Träger, Dreieckträger gegebenen speziellen Formeln zu berechnen. Im übrigen können selbstverständlich für alle Trägeröffnungen bei voller Wand die unter Balken, Biegung, Blechträger, bei Fachwerken die unter Fachwerke, statisch bestimmte, mehrfachen Systems, statisch unbestimmte, angeführten Formeln und Methoden zur Verwendung kommen und nach dem unter Grenzwerte, Einflußlinien Gesagten auch die Grenzwerte der Beanspruchungen und Stützenreaktionen ermittelt werden, sobald letztere oder die Momente M, M' über den Stützen der einzelnen Oeffnungen für beliebige Belastung bekannt sind. Diese sollen deshalb zunächst ausgedrückt werden. Dabei wird vorausgesetzt, daß in den Vertikallinien durch die Stützpunkte und Gelenke Knotenpunkte mit Uebertragung der Fahrbahnlast liegen, falls letztere nicht direkt auf die Hauptträger wirkt.

Die Momente über den Zwischenstützen ergeben sich aus den Verhältnissen der Oeffnungen mit Zwischengelenken und sind nur von deren Belastung abhängig. M, M' seien die Momente über den Stützen, welche einer beliebigen Oeffnung l mit Zwischengelenken anliegen. Dann entstehen durch eine auf die Oeffnung gleichmäßig verteilte Last von g pro Längeneinheit:

und durch beliebige Lasten P₁, P₂ ..., welche bei beliebigen Abszissen a₁, a₂ ... (Horizontalabstände vom unmittelbar vorausgehenden Stützpunkte, Fig. 16) auf den Träger oder die Fahrbahn kommen:

Die Summen Σ sind auf alle Lasten zwischen den beigesetzten Grenzen zu erstrecken. Lasten außerhalb der Strecke von 0 bis t sind auf M, Lasten außerhalb der Strecke von r bis l sind auf M' ohne Einfluß. Für eine Anfangsöffnung mit Zwischengelenk hat man r = 0, M = 0, für eine Endöffnung mit Zwischengelenk t = l, M' = 0. Mit 1.–3. werden z.B. die unter Balken, Balkenfachwerke, Bd. 1, S. 503, 526, gegebenen Formeln verwendbar. Ableitung vorstehender und der folgenden Formeln s. [10], § 57.

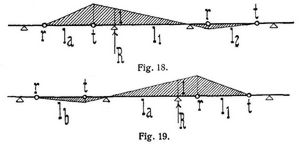
In Fig. 18, 19 sind die Einflußlinien der Reaktion R einer beliebigen Stütze für die beiden möglichen Fälle dargestellt, daß die Oeffnung vor bezw. nach der Stütze Zwischengelenke enthält (Oeffnungen mit und ohne Zwischengelenke alternieren miteinander, Fig. 3–9). Diese Einflußlinien ergeben sich, nachdem über der fraglichen Stütze die Ordinate 1 angetragen ist, in der aus Fig. 18, 19 ersichtlichen Weise. Ordinaten und Flächenteile oberhalb der Abszissenachse sind als positiv, solche unterhalb derselben als negativ anzusehen, Lasten außerhalb der durch die Einflußlinie eingenommenen Strecken sind ohne Einfluß auf die betreffende Stützenreaktion. Für eine Anfangsstütze fallen die in Fig. 18, 19 vor der Stütze liegenden Flächenteile selbstverständlich weg, für eine Endstütze gilt das gleiche für die Flächenteile nach der Stütze, ohne daß hierdurch an der Allgemeinheit der Darstellung etwas geändert wird. Man erhält nun die Reaktion einer beliebigen Stütze durch eine auf die ganze Länge der beitragenden Strecken gleichmäßig verteilte Last von g pro Längeneinheit (über verschiedene gleichmäßig verteilte Lasten in den einzelnen Oeffnungen s. [10], S. 192), wenn F den algebraischen Gesamtinhalt der Einflußfläche bezeichnet:

und durch beliebige Lasten P₁ P₂ ..., welche in beliebigen Knotenpunkten oder Fahrbahnpunkten angreifen, wenn b₁, b₂ ... die positiven oder negativen Ordinaten der Einflußfläche daselbst bedeuten:

wobei die Summation auf alle beitragenden Lasten P zu erstrecken ist. Die F, b können aus der Figur abgegriffen oder nach derselben berechnet werden.

Die Stützenreaktionen lassen sich auch ohne Rücksicht auf die Einflußlinien ausdrücken. Es mögen sich Größen und Ausdrücke mit den Indices a und b auf die erste und zweite der fraglichen Stütze vorangehende Oeffnung l_a und l_b, solche mit den Indices 1 und 2 auf die erste und zweite ihr nachfolgende Oeffnung l₁ und l₂ beziehen (Fig. 18, 19). Dann hat man durch eine gleichmäßig verteilte Last von g pro Längeneinheit auf allen beitragenden Strecken (über verschiedene gleichmäßig verteilte Lasten in den einzelnen Oeffnungen s. [10], S. 192) für l₁ mit oder l_a ohne Zwischengelenk:

[365] Durch beliebige Einzellasten P₁, P₂ ..., welche in den einzelnen Oeffnungen bei Abszissen a₁, a₂ ... (Abstände von den zunächst vorausgehenden Stützpunkten) am Träger oder auf der Fahrbahn angreifen, ergeben sich für l₁ mit oder l_a ohne Zwischengelenk:

für l₁ ohne oder l_a mit Zwischengelenk:

Die Indices der Klammerausdrücke in 8., 9. deuten an, auf welche Oeffnungen sich die nicht durch besondere Indices gekennzeichneten Größen in den Klammern beziehen.

Im vorstehenden ist angedeutet, wie durchlaufende Gelenkträger nach Methoden und Formeln zu berechnen sind, welche auch für andre Träger zur Verwendung kommen. Indessen lassen sich für durchlaufende Gelenkträger der besprochenen statisch bestimmten Art und einfachen Fachwerksystems (s. Fachwerke) auch Ausdrücke für die Stabkräfte bei beliebiger Belastung und für die Grenzwerte der Stabkräfte bei gleichmäßig verteilter bewegter Last und bewegten Radlastzügen ableiten, nach welchen diese Stabkräfte und Grenzwerte bei bekannten Lasten ohne weiteres berechnet werden können. Man findet solche Formeln für Fachwerke einfachen Systems mit Vertikalen (Ständerfachwerke) und beliebigen Gurtungsformen in [10], §§ 59–61, Beispiele hierzu [11], 75, 78, 79, 82, 83 (Dachbinder B. 75), für Parallelträger einfachen Systems mit Vertikalen in [10], §§ 63, 64, 65, Beispiele hierzu [11], B. 76, 77, 80, 81. Bei einfachem System ohne oder mit Vertikalen sind die Stabkräfte nach der Bd. 3, S. 549, angeführten Momentenmethode proportional den Schnittmomenten M_s, und ihre Grenzwerte proportional den Grenzwerten von M_s. Die Werte von M_s für beliebige Belastung, ihre Einflußlinien und die Grenzwerte von M_s für gleichmäßig verteilte bewegte Last und bewegte Radlastzüge sind in [10], 57–59, gegeben. Bei vertikalen Schnitten s = x und Momentendrehpunkten u = x gelten diese Formeln auch für vollwandige Träger.

Literatur: [1] Ritter, A., Elementare Theorie und Berechnung eiserner Dach- und Brückenkonstruktionen, Hannover 1.863, S. 187 (3. Aufl., Hannover 1873, S. 214). – [2] Beschreibung des am 6. Dezember 1866 dem Ingenieur Gerber verliehenen Patentes auf Balkenträger mit freiliegenden Stützpunkten, Zeitschr. des bayr. Ingen.- u. Arch.-Vereins 1870, S. 75. – [3] Reymann, Brücke nach Gerbers System, Zeitschr. d. Arch.- u. Ingen.-Vereins zu Hannover 1875, S. 167. – [4] Meyer und Hinrich, Der eiserne Ueberbau der Warthebrücke bei Posen, Zeitschr. f. Bauwesen 1877, S. 41. – [5] Winkler, Theorie der Brücken, II, Theorie der gegliederten Balkenträger, Wien 1881, S. 221. – [6] Der Gerbersche Träger mit freischwebenden Stützpunkten im Hochbau, Zeitschr. f. Baukunde 1882, S. 543. – [7] Heyn, Der Gelenkträger im Hochbau, Deutsche Bauztg. 1882, S. 203. – [8] Schneider, Die neue Niagarabrücke, Zeitschr. d. Vereines deutscher Ingen. 1884, S. 385. – [9] Post, Ein Vorschlag zum Bau billiger Brücken, Zentralblatt der Bauverwaltung 1886, S. 57, 231. – [10] Weyrauch, Theorie der statisch-bestimmten Träger für Brücken und Dächer, Leipzig 1887, S. 186. – [11] Ders., Beispiele und Aufgaben dazu, Leipzig 1888, S. 322. – [12] Barkhausen, Die Forth-Brücke, Zeitschr. d. Vereines deutscher Ingen. 1888, S. 912. – [13] Ders., Der Bau eiserner Brücken in den letzten Jahren und seine Ergebnisse, Zeitschr. d. Vereines deutscher Ingen. 1889, S. 909, 938, 995, 1037, 1094. – [14] Mehrtens, Ueber den Plan einer Eisenbahnbrücke zwischen England und Frankreich, Zentralblatt der Bauverwaltung 1889, S. 458, 471, 479 (nach Pont sur la Manche, Avant-Projets de MMr. Schneider, Usines du Creusot, et Hersent, entrepreneur des travaux publics, Paris et Londres 1889). – [15] Struckel, Die Forth-Brücke bei Queensferry, Allgem. Bauztg. 1890, S. 65, 73, 84. – [16] Westhofen, The Forth Bridge, Engineering 1890, I, S. 213–283, 303 (Historisches über Gelenkträger S. 217, auch Engineering 1881, II, S. 475). – [17] Lang, Die Entwicklungsgeschichte der Spannwerke des Bauwesens, Riga 1890, S. 153. – [18] Klett, Die Kragträgerbrücken in Deutschland, Zeitschr. d. Vereines deutscher Ingen. 1891, S. 85. – [19] Hübner, Durchgehende Träger mit Querkraftnullfeldern, Zeitschr. f. Bauwesen 1891, S. 552. – [20] Gärtner, Der Donauübergang Fetesti-Cernavoda, Allgem. Bauztg. 1896, S. 25. – [21] Gandard, Application du Systeme Cantilever aux halles métalliques; halle des machines de l'Exposition suisse en 1896, Paris, imprimerie Chaix, 1897. – [22] Müller-Breslau, Ueber die Berechnung statisch unbestimmter Auslegerbrücken, Zentralblatt der Bauverwaltung 1897, S. 503. – [23] Müller-Breslau, Der Kaisersteg über die Spree bei Oberschönweide, Zeitschr. f. Bauwesen 1900, S. 65, 291. – [24] Müller-Breslau, Die graphische Statik der Baukonstruktionen, I, Leipzig 1901, S. 330, 427; I, 1903, S. 167, 294. – [25] Weyrauch, Ueber die Zunahme der Brückenspannweiten im 19. Jahrhundert, Zeitschr. f. Bauw. 1901, S. 465, 617. – [26] Handbuch der Ingenieurwissenschaften, Bd. 2, Der Brückenbau, 2. Abt., Leipzig 1901, S. 334; 5. Abt., Leipzig 1906, S. 114 (ausgekragte Bogenträger). – [27] Melan und Swoboda, Der Bau der Erzherzog-Ludwig-Viktor-Brücke über die Salzach in Salzburg, Allgem. Bauztg. 1904, S. 1. – [28] Degener, Der Wettbewerb für eine Straßenbrücke über den Rhein zwischen Ruhrort und Homberg, Zentralblatt der Bauverwaltung 1904, S. 270, 347, 372, 395, 425, 492, 622. – [29] Horowitz, Die größte Auslegerbrücke der Welt, Zeitschr. d. österr. Ingen.- u. Arch.-Vereins 1905, S. 711. – [30] Müller-Breslau, Ueber die Berechnung von Schiffbrücken mit Gelenken, Zeitschr. f. Bauwesen 1906, S. 151.

Weyrauch.

Fig. 1., Fig. 2.

Fig. 3., Fig. 4.

Fig. 5., Fig. 6.

Fig. 7.

Fig. 8., Fig. 9.

Fig. 10.

Fig. 11.

Fig. 12.

Fig. 13.

Fig. 14.

Fig. 15.

Fig. 16., Fig. 17.

Fig. 18., Fig. 19.