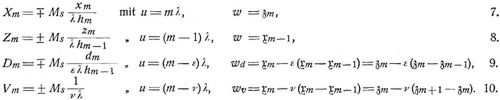- Fachwerke, statisch bestimmte
Fachwerke, statisch bestimmte. Ein Fachwerk (s.d.), Fachwerkträger, heißt statisch bestimmt, wenn sich seine Stützenreaktionen und Stabkräfte aus statischen Bedingungsgleichungen allein, ohne Zuhilfenahme der Elastizitätslehre bestimmen lassen. Die Berechnung wird hierdurch leichter und zuverlässiger als bei statisch unbestimmten Fachwerken, während ein weiterer Vorzug der statisch bestimmten Fachwerke darin besteht, daß kleine Verrückungen der Stützpunkte, gleichmäßige Temperaturänderungen der einzelnen Stäbe und kleine Abweichungen der Stablängen gegen deren planmäßige Werte keinen in Betracht kommenden Einfluß auf die Beanspruchungen ausüben (vgl. Fachwerke, statisch unbestimmte).
Bedingungen der statischen Bestimmtheit und Stabilität sowie allgemeine Gesichtspunkte bezüglich der Berechnung von Fachwerken s. Fachwerk, über die Berechnung von Balkenfachwerken und Bogenfachwerken mit Vertikalen, wenn nur vertikale Aktivkräfte (Lasten) wirken, vgl. Balkenfachwerke Bogenfachwerke und eventuell Dreieckträger, Parabelträger, Paulische Träger, Schwedler-Träger, über Parallelträger und Polonceautrager s. unter diesen Stichworten. Allgemeines bezüglich der Berechnung von Grenzwerten bei bewegter Last s. Grenzwerte, Einflußlinien. Die Ermittlung der Formänderungen ist unter Einsenkung und Fachwerke, statisch unbestimmte, besprochen, die Berechnung von Fachwerken mehrfachen Systems auf Grund der Zerlegung in einfache Systeme unter Fachwerke mehrfachen Systems. Im folgenden handelt es sich um die Berechnung der Stabkräfte (Grundspannungen) beliebiger statisch bestimmter und stabiler Fachwerke. Der betreffende Träger sei nach Einwirkung irgend welcher äußerer Kräfte (s. Bd. 1, S. 103) zum Gleichgewichte gelangt. Die Verrückungen der Knotenpunkte werden den anfänglichen Abmessungen des Fachwerks gegenüber als verschwindend klein vorausgesetzt.
Knotenpunktmethode. Bezüglich eines rechtwinkligen Koordinatensystems in fester Lage gegen die anfängliche Gruppierung der Knotenpunkte seien xm, ym, zm die Koordinaten eines Knotenpunkts m und xn, yn, zn diejenigen eines Knotenpunktes n, der mit m durch einen Stab der anfänglichen Länge l und schließlichen Stabkraft S verbunden ist. Xm, Ym, Zm mögen die resultierenden Komponenten der in m angreifenden äußeren Kräfte in den Richtungen x, y, z bezeichnen. Werden dann die S als positiv oder negativ angenommen, je nachdem sie Zug oder Druck bedeuten, so bestehen fürs Gleichgewicht am Knotenpunkte m die Bedingungsgleichungen [5], S. 49, [6], S. 61:
worin die Summen Σ/m sich auf sämtliche in m eintreffende Stäbe beziehen. Für ebene Fachwerke hat man, wenn das Koordinatensystem in die Trägerebene gelegt wird:
Bei k Knotenpunkten liefert die Statik 3 k bezw. 2 k solcher Gleichungen, welche durch die darin auftretenden Größen erfüllt sein müssen und zur Bestimmung von Unbekannten dienen[549] können. Unbekannt sind aber die r voneinander unabhängigen Reaktionskomponenten, welche Größe und Richtung sämtlicher Stützenreaktionen bestimmen, und die s wirksamen Stabkräfte (vgl. Fachwerk). Da nun für statisch bestimmte stabile Fachwerke gerade 3k = r + s (im Räume) bezw. 2k = r + s (in der Ebene) ist, so genügen die vorhandenen 3k Gleichungen 1. bezw. 2k Gleichungen 2., um sämtliche unbekannte Stabkräfte und Stützenreaktionen zu bestimmen. – Das vorstehende Verfahren kommt besonders bei räumlichen Fachwerken zur Verwendung, kann sich aber auch mitunter bei ebenen Fachwerken empfehlen. Anwendungen des Verfahrens [6] B. 13–16, A. 16–19, 24, 28, 39, 46, 47, 49. Im folgenden handelt es sich um ebene Fachwerke. Ueber räumliche Fachwerke s. [8], [9], [11], [12].
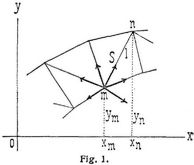
Schnittmethode. Man denke sich durch das eben vorausgesetzte Fachwerk einen beliebig geformten Schnitt s so gelegt, daß das Fachwerk in zwei Teile, I und II, getrennt erscheint (Fig. 2). Für diejenigen äußeren Kräfte des Trägers, welche am Trägerteil I wirken, seien Hs die resultierende Horizontalkraft, Vs die resultierende Vertikalkraft, Ms das resultierende Moment hinsichtlich eines beliebig gewählten Drehpunkts in der Trägerebene. Mit Hs, Vs, Ms müssen diejenigen Kräfte im Gleichgewicht sein, welche als Stabkräfte vom Trägerteil II aus auf I wirken (also für I ebenfalls äußere Kräfte darstellen). Wir denken uns dieselben zunächst wie Zugkräfte vom Schnitte s weggerichtet, so daß sie Druck bedeuten, wenn sie sich negativ ergeben. Ein rechtwinkliges Koordinatensystem in fester Lage gegen die anfängliche Gruppierung der Knotenpunkte werde in der Trägerebene so angenommen, daß die positiven Richtungen der Koordinatenachsen mit den positiven Richtungen von Hs, Vs übereinstimmen. Das Moment Ms soll als positiv gelten, wenn es, wie der Zeiger der Uhr, rechts um den gewählten Drehpunkt der Koordinaten u, w dreht. Bezeichnen dann für die vom Schnitte s getroffenen Stäbe X, Y, Z, ... die Stabkräfte, ξ, η, ζ, ... die Winkel ihrer Richtungen mit der positiven Richtung der Abszissenachse und x, y, z, ... ihre Hebelarme in Hinsicht des Punktes u, w, so lauten die Bedingungen fürs Gleichgewicht am Trägerteil I (Fig. 2, vgl. [5], S. 54):
Die Momente Xx, Yy, Zz, ... erhalten das obere oder untere Vorzeichen, je nachdem die vom Trägerteil I weggerichteten Kräfte X, Y, Z, ... (Fig. 2) auf Drehung rechts oder links um u, w wirken. Aus den Gleichungen 3. für einen Schnitt s lassen sich im allgemeinen drei unbekannte Größen berechnen. Man hat also nach Ermittlung der Stützenreaktionen, wozu Bedingungsgleichungen für sämtliche äußere Kräfte am Träger zu dienen pflegen, die Schnitte s der Reihe nach so zu legen, daß durch einen Schnitt s nicht mehr als drei Stäbe mit unbekannten Stabkräften getroffen werden (die Beanspruchungen der etwa noch weiter getroffenen müssen aus den Gleichungen für vorausgegangene Schnitte bestimmt sein). Die Hs, Vs, Ms in 3. wird man meist am einfachsten für den gegebenen Fall numerisch einführen. Bezüglich allgemeiner Formeln für dieselben s. Schnittkräfte und [5] §§ 7, 8, 10 und [6] A. 4, 5 mit Beispielen [6] B. 40, 58, 86. Anwendungen obiger Gleichungen [6] B. 17 und A. 20, 21.
Momentenmethode (Rittersche Methode). Die Bestimmung einer Stabkraft aus 3. erfordert im allgemeinen die Auflösung dreier Gleichungen. Dies ist häufig unbequem, insbesondere dann, wenn für eine gewisse Belastung nur eine Stabkraft interessiert (z.B. bei Berechnung von Grenzwerten, s.d.). Zur Bestimmung dieser einen Stabkraft würde auch eine Gleichung genügen, vorausgesetzt, daß dieselbe von unbekannten Kräften nur die gesuchte enthält. Dies ist bei bekanntem Ms stets erreichbar, wenn die übrigen von s getroffenen unbekannten Stabkräfte sich in einem Punkte schneiden, also beispielsweise wenn der Schnitt s, wie auch für die Berechnung nach 3. nötig, nur drei Stäbe mit unbekannten Beanspruchungen trifft. Da nämlich die Wahl des Momentendrehpunktes freisteht, so legt man ihn nach dem Vorgange von A. Ritter [1] in den Durchschnitt der nichtgesuchten unbekannten Stabkräfte. Bezeichnet B das Moment der etwa von Schnitt s getroffenen bekannten Stabkräfte für den gewählten Drehpunkt, so folgen aus der letzten Gleichung 3.,
u.s.w. Trifft s, wie vielfach an Trägerenden, nur zwei unbekannte Stabkräfte, so kann bei Berechnung der einen der Drehpunkt in einen beliebigen Punkt der andern gelegt werden. Anwendungen des vorgehenden Verfahrens s.u.a. [6], B. 18–22 und A. 22, 23. Ausdrücke des Momentes Ms und seiner Grenzwerte für bewegte Last (womit sich auch aus 4.–6. die Grenzwerte der Stabkräfte ergeben) bei beliebigen Systemen einfacher Balkenfachwerke [5], §§ 23–25, durchlaufender Gelenkträger [5], §§ 57–59, von Bogenfachwerken mit drei Gelenken [5], 66–68, in weiteren Fällen [5], §§ 76, 80–82, 85. Betreffend Ms s. a. die Bemerkung am Schlusse der vorigen Methode.
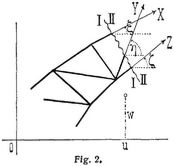
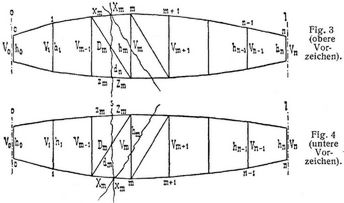
[550] Einfaches System mit Vertikalen (Ständerfachwerke). Von allen Fachwerksystemen kommt bei weitem am meisten das einfache System mit Vertikalen zur Verwendung. Die Ermöglichung bequemer Anschlüsse der Querträger und zweckmäßiger Uebertragung der Kräfte von letzteren wie von den vertikalen und horizontalen Querverbänden in die Hauptträger und bis zu den Auflagern pflegt neben anderm dafür zu sprechen. Im folgenden mag es sich um statisch bestimmte oder statisch unbestimmte, einfache oder durchlaufende Balkenfachwerke und Bogenfachwerke dieses Systems mit gleich oder verschieden hohen Stützpunkten handeln. Ueber direkt verwendbare Formeln für spezielle Fälle s. oben. – Die Trägerlänge zwischen zwei aufeinander folgenden Stützpunkten (bei einfachen Trägern die ganze Trägerlänge) sei durch Vertikalen in n Felder von gleichen Längen λ geteilt. Spannweite der betrachteten Oeffnung also l = n λ In jedem Felde befindet sich eine wirksame Diagonale (Gegendiagonalen zugelassen, da alsdann auch stets nur eine der beiden Diagonalen wirksam ist oder sein soll). Die Diagonale kann zweierlei Stellungen in ihrem Felde einnehmen. Wir führen die in Fig. 3, 4 ersichtlichen Bezeichnungen ein, wonach die Stabkräfte derjenigen Gurtung mit X bezeichnet sind, welche man einer Diagonale nach der Seite von Auflager 0 hin folgend trifft. xm, zm, dm, hm seien die Längen derjenigen Stäbe, welche durch Xm, Zm, Dm, Vm beansprucht sind, und xm, zm die Ordinaten der Knotenpunkte m in X-Gurtung und Z-Gurtung bezüglich eines rechtwinkligen Koordinatensystems mit dem Ursprung in Stützpunkt 0 und horizontaler Abszissenachse. Dann gelten in allen das fragliche Fachwerksystem betreffenden Ausdrücken der Stabkräfte die oberen Vorzeichen bei obenliegender X-Gurtung (Fig. 3), die unteren Vorzeichen bei unten liegender X-Gurtung (Fig. 4). Die Anwendung der obigen Momentenmethode liefert folgende Formeln, wobei u, w die Koordinaten des Drehpunkts für das Moment Ms bedeuten (Näheres s. [5], § 16):
In diesen Gleichungen hat man bei beliebigen Gurtungsformen:
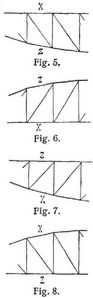
und speziell bei horizontaler X-Gurtung (Fig. 5, 6):
bei horizontaler Z-Gurtung (Fig. 7, 8);
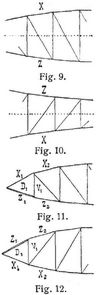
bei symmetrischen Gurtungen (zu einer beliebigen Horizontalen, Fig. 9, 10);
Die Formeln für Xm, Zm, Dm, in denen sich Ms auf einen Schnitt s durch das m te Feld bezieht (Fig. 3 und 4), gelten auch, wenn die Stellung der Diagonalen wechselt (die X-Gurtung also einmal oben, einmal unten liegt); dagegen ist die Formel für Vm, in der Ms einem Schnitt s durch die mit Xm, Vm, Zm + 1 beanspruchten Stäbe entspricht (Fig. 3 und 4), an die Voraussetzung gebunden, daß sich zu beiden Seiten der Vertikale m Felder der betrachteten Oeffnung l mit Diagonalen gleicher Stellung oder ohne Diagonalen (Fig. 11, 12) befinden. In andern Fällen, wie sie insbesondere an den Enden und in den Mitten der Oeffnungen vorkommen, führen meist die Gleichgewichtsbedingungen für einen die Vertikale begrenzenden Knotenpunkt schnell zum Ziel- (z.B. bei horizontaler Gurtung die Bedingung: Summe aller im Knotenpunkte angreifenden Vertikalkräfte gleich Null). Direkt verwendbare Formeln für die Beanspruchungen von[551] End- und Mittelvertikalen sowie deren Grenzwerte bei bewegter Last s. [6] A. 19, 24, 28, 39, 42. Neben den angeschriebenen Gleichungen gelten allgemein:
Beispiele der Anwendung von 7.–10. für beliebig gerichtete Aktivkräfte (schiefen Winddruck) s. [6] B. 40, 58, 86, Spezialisierung der Formeln für beliebige Belastung, gleichmäßig verteilte Last, Radlastzüge und die Grenzwerte in den wichtigsten Fällen, insbesondere für einfache Balkenfachwerke, durchlaufende Gelenkträger, einfache und durchlaufende Bogenfachwerke in [5], Beispiele der Anwendung für diese und andre Fälle in [6]. Bezüglich Ms, Hs vergl. das oben am Schlusse der Schnittmethode Gesagte, bezüglich spezieller Formeln für Balken- und Bogenfachwerke s. auch die obige Einleitung. Wenn am Träger nur vertikale Aktivkräfte (Lallen) wirken, dann ist in allen Schnitten s für Balkenfachwerke Hs = 0, für Bogenfachwerke Hs = H von gleichem Wert (Horizontalschub).
Literatur: [1] Ritter, A., Elementare Theorie und Berechnung eiserner Dach- und Brückenkonstruktionen, Hannover 1863 (4. Aufl. 1880). – [2] Foeppl, Theorie des Fachwerks, Leipzig 1880. – [3] Winkler, Theorie der Brücken, II: Theorie der gegliederten Balkenträger, Wien 1881. – [4] Henneberg und Smreker, Lehrbuch der technischen Mechanik, I: Statik der starren Systeme, Darmstadt 1886. – [5] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887. – [6] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888. – [7] Ritter, W., Anwendungen der graphischen Statik, II: Das Fachwerk, Zürich 1890. – [8] Foeppl, Das Fachwerk im Räume, Leipzig 1892. – [9] Zimmermann, Ueber Raumfachwerke, neue Formen und Berechnungsweisen für Kuppeln und sonstige Dachbauten, Berlin 1901. – [10] Müller-Breslau, Die graphische Statik der Brückenkonstruktionen I, Leipzig 1901. – [11] Handbuch der Ingenieurwissenschaften, Bd. 2: Der Brückenbau, 2. Abteilung (Theorie der eisernen Balkenbrücken), Leipzig 1901; 6. Abteilung (eiserne Brückenpfeiler), Leipzig 1903. – [12] Müller-Breslau, Die neueren Methoden der Festigkeitslehre, Leipzig 1904 (Abschnitt IV: Das räumliche Fachwerk). – [13] Ostenfeld, Technische Statik, Leipzig 1904. – [14] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, II: Statisch bestimmte Träger, Leipzig 1904. – Weitere Literatur s. Fachwerke, auch mehrfachen Systems, und die obenerwähnten Stichworte.
Weyrauch.
http://www.zeno.org/Lueger-1904.