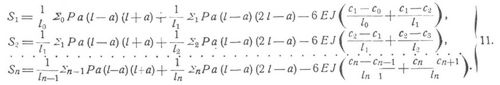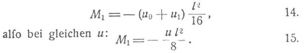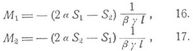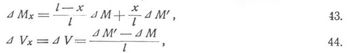Balken, durchlaufende

Balken, durchlaufende (kontinuierliche). Durchlaufende oder kontinuierliche Balken heißen solche Balken (s.d.), die ungetrennt über mehr als eine Oeffnung reichen. Formeln für dieselben bei beliebiger Belastung sind unter Balken, Biegung, Einsenkung, Elastische Linie, Fachwerke (statisch unbestimmte) gegeben, wonach mit Rücksicht auf das unter Belastung der [508] Träger Gesagte auch Ausdrücke für spezielle Belastungen entnommen werden können. Weitere Formeln folgen unten. Kontinuierliche Balken kommen im Hochbau und Brückenbau vor, sie sind mitunter nicht vermeidbar (Drehbrücken, schiefe Endquerträger wie in [3], S. 151, u.s.w.). Mehreren einfachen Balken von annähernd gleichen Spannweiten gegenüber können bei Brücken folgende Vorteile derselben in Betracht kommen: a) Materialersparnis für die Gurtungen, meist 20–24%; b) geringere Einsenkungen und größere Steifigkeit gegen seitliche Einwirkungen; c) Möglichkeit schmaler Zwischenstützen (z.B. eiserner Säulen) in Straßen, Bahnhöfen u.s.w.; d) Einfachheit der Konstruktion bei schiefen Brücken und Oeffnungen mit verschiedenen Straßenfluchten (die Hauptträger laufen über alle Ungleichheiten weg, die Querträger können rechtwinklig zu denselben bleiben); e) Erleichterung der Aufstellung, wenn die Herstellung von Gerüsten untunlich ist (die auf horizontaler Unterlage fertiggestellten Träger werden über die Stützen weggeschoben). Dagegen sind folgende Nachteile anzuführen: a) die umständlichere und mit Rücksicht auf die Voraussetzungen der Elastizitätslehre weniger zuverlässige Berechnung; b) der Einfluß unbeabsichtigter Aenderungen der Stützhöhen auf die Beanspruchungen (s. unten); c) der Einfluß gewisser Temperaturänderungen auf die Beanspruchungen (s. unten).

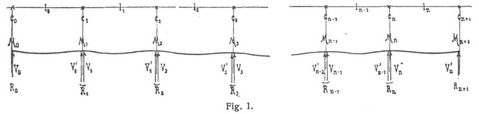
Gewöhnlichster Fall. Es handle sich um einen Träger mit n Zwischenstützen und frei drehbaren Enden, dessen Stützpunkte in einer horizontalen oder geneigten Geraden liegen (die Stützpunkte sind immer in der Stabachse zu denken), während die Belastung auf die Länge je einer ganzen Oeffnung gleichmäßig verteilt und u pro Längeneinheit ist. In praktischen Fällen hat man dann entweder u = g (Eigengewicht der Konstruktion) oder u = q = g + p (Vollbelastung). Für die n Stützenmomente bestehen n Gleichungen von der Form (Bezeichnungen s. Fig. 1, 2, Formeln zu direkter Berechnung beliebiger Stützenmomente unten):

M_{r – 1}l_{r – 1} + 2M_r(l_{r – 1} + l_r) + M_{r + 1} l_r = – ¹/₄ (u_{r – 1}l³_{r – 1} + u_rl³_r)

1.

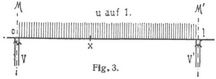
wobei der Einfluß der Vertikalkraft V_x vernachlässigt ist (s. im vorletzten Absatz des Artikels Balken und unten vor Gleichung 10.). Die Momente über den Endstützen sind gleich 0. In jeder Oeffnung l (Fig. 3) hat man die Vertikalkräfte unmittelbar bei den Stützen, zwischen denen die Werte aller andern V_x liegen:

V₀ = 1/l[M' – M + (ul²)/2] = V,

2.

V_l = 1/l[M' – M – (ul²)/2] = – V'.

3.

Moment und Vertikalkraft in einem beliebigen Querschnitt x:

M_x = M + Vx – (ux²)/2 = [(l – x)/l]M + (x/l)M' + (u/2)x(l – x),

4.

V_x = V – ux = (M' – M)/l + u(l/2 – x)

5.

unter M, M' die Stützenmomente bei x = 0 und x = l verstanden (Fig. 3). Abszisse x = μ des größten positiven Moments in der Oeffnung:

μ = V/u = l/2 + (M' – M)/ul,

6.

Wert desselben:

Mμ = M + (uμ²)/2.

7.

Reaktion einer beliebigen Stütze r:

R_r = V_r + V'_{r – 1}.

8.

Reaktionen der Endstützen:

R₀ = V₀,

R_{n + 1} = V'_n.

9.

Es kommt vor, daß eine solche Endreaktion bei gewissen Belastungen negativ wird, in welchem Falle zur Vermeidung eines Abhebens des Trägers von der Stütze für die Möglichkeit negativer (d.h. von oben nach unten wirkender) Stützenreaktionen gesorgt werden muß, also das betreffende Trägerende zu verankern ist. Bezüglich der Spannungen s. Biegung I, bezüglich der Einsenkung s. dieses Stichwort.

[509] Weiteres über die Stützenmomente. Die allgemeinen Formeln für die Stützenmomente sind ohne den meist vernachlässigten Einfluß der Vertikalkraft V_x unter Balken, und mit Berücksichtigung dieses besonders für die Formänderungen oft erheblichen Einflusses unter Elastische Linie gegeben. Wir wollen hier Formeln ohne den Einfluß von V_x für frei drehbare Trägerenden zusammenstellen, wie sie bei den Hauptträgern von Balkenbrücken stets vorausgesetzt werden. Für n Zwischenstützen existieren n Stützenmomente und für diese n Gleichungen von der Form

M_{r – 1}l_{r – 1} + 2M_r(l_{r – 1} + l_r) + M_{r + 1}l_r = – S_r,

10.

worin bei beliebiger Belastung und beliebigen Stützhöhen (innerhalb der für horizontale Balkenträger gültigen Grenzen, s. Balken, Biegung I):

Speziellere Ausdrücke für die Summen Σ₀, Σ₁, ... Σ_n, die sich auf alle Lasten in den Oeffnungen l₀, l₁, ... l_n beziehen, sind unter dem Stichwort Belastung der Träger gegeben. Für den gewöhnlichen Fall, daß die Stützpunkte in einer horizontalen oder geneigten Geraden liegen, fallen die Glieder mit dem Faktor 6 EJ weg. Man hat dann in 10. für gleichmäßig verteilte Lasten auf die Länge je einer ganzen Oeffnung (u₀, u₁, ... u_n pro Längeneinheit in l₀, l₁, ... . l_n):

Die Berechnung der Stützenmomente aus 10. hat bei mehreren Zwischenstützen das Unbequeme, daß die n Gleichungen nach sämtlichen n Stützenmomenten aufgelöst werden müssen. Dies fällt besonders dann ins Gewicht, wenn für gewisse Belastungsfälle nur einzelne Stützenmomente interessieren (ungünstigste Belastungen). Wir wollen deshalb für symmetrische Balken (Spannweiten symmetrisch zur Trägermitte) mit frei drehbaren Enden noch Formeln zu unmittelbarer Berechnung jedes einzelnen Stützenmoments geben.

I₀ = 0, I'₀ = ⁴/₅ l, I₁ = ¹/₅ l, l' = l

Syminetrischer Träger mit 2 Oeffnungen (Fig. 4). Für beliebige Belastung und beliebige Stützhöhen hat man:

und speziell für gleichmäßig verteilte Lasten auf die Länge je einer ganzen Oeffnung und Stützpunkte in einer Geraden

Symmetrischer Träger mit 3 Oeffnungen (Fig. 5). Mit den abkürzenden Bezeichnungen

α = 1 + σ, β = 1 + 2σ, γ = 3 + 2σ

hat man für beliebige Belastung und beliebige Stützhöhen:

und speziell für gleichmäßig verteilte Lasten auf die Länge je einer ganzen Oeffnung und Stützpunkte in einer Geraden:

M₁ = – (2ασ³u₀ + βu₁ – σ³u₂)l²/(4βγ),

18.

M₂ = (2ασ³u₂ + βu₁ – σ³u₀)l²/(4βγ),

19.

wonach bei gleichen u:

M₁ = M₂ = – (1 + σ³)/(3 + 2σ)(ul²)/4.

20.

Symmetrischer Träger mit 4 Oeffnungen (Fig. 6). Mit den abkürzenden Bezeichnungen

α = 1 + σ

β = 3 + 4σ

γ = 7 + 8σ

δ = 1 + 2σ

ε = 5 + 6σ

hat man für beliebige Belastung und beliebige Stützhöhen:

[510] und für gleichmäßig verteilte Lasten auf die Länge je einer ganzen Oeffnung und Stützpunkte in einer Geraden:

wonach bei lauter gleichen u:

Symmetrischer Träger mit 5 Oeffnungen (Fig. 7).

Mit den abkürzenden Bezeichnungen

hat man für beliebige Belastung und beliebige Stützhöhen:

und für gleichmäßig verteilte Lasten auf die Länge je einer ganzen Oeffnung und Stützpunkte in einer Geraden:

wonach bei lauter gleichen u:

Sind alle Felder gleichlang, dann hat man in den für symmetrische Träger von 3–5 Oeffnungen gegebenen Formeln σ = 1, doch kommt dieser Fall verhältnismäßig selten vor.

Bewegte Last. Wir fassen zunächst den einfachsten Fall ins Auge, daß die bewegte Last auf die ergriffene Strecke gleichmäßig verteilt ist. Gilt letzteres auch Tür das Eigengewicht der Konstruktion, so genügen zur Berechnung der untenerwähnten Grenzwerte die Formeln 1.–9. Für die Stützenmomente symmetrischer Träger mit 2–5 Oeffnungen wird man jedoch die bequemeren Formeln 14.–15., 18.–20., 24.–28., 33.–38. verwenden. In jeder Oeffnung l eines kontinuierlichen Balkens befinden sich zwei nur von den Spannweiten abhängige Punkte I, I', die in den beiden äußersten Dritteln vom l liegen und die Eigenschaft haben, daß das Moment M_x bei x = I durch beliebige Belastung aller folgenden, das Moment bei x = I' durch beliebige Belastung aller vorhergehenden Oeffnungen nicht geändert wird. Die Abszissen dieser Punkte,[511] die Inflexionspunkte (nach Culmann) oder Fixpunkte (nach Mohr) der betreffenden Oeffnungen heißen, sind in Fig. 4–7 für symmetrische Träger von 2–5 Oeffnungen mit frei drehbaren Enden über ihren Oeffnungen angegeben. Die abkürzenden Bezeichnungen α, β, γ, ... wurden schon bei den Ausdrücken der Stützenmomente verwendet. Ueber die Berechnung der I, I' für unsymmetrische und an den Enden eingespannte Träger s. [3], S. 51, 99, 106. Bei den folgenden Angaben der Belastungen für die Grenzwerte verstehen wir unter vollbelasteten und unbelasteten Oeffnungen solche, die auf ihrer ganzen Länge durch die feste Last und bewegte Last bezw. durch die feste Last allein ergriffen sind. Letztere ist ganz beliebig, während die gleichmäßig verteilte bewegte Last in jeder Oeffnung einen andern Wert haben kann. In den beigesetzten Figuren bedeuten fette Striche Vollbelastung, feine Striche Eigengewicht allein.

a) Stützenmomente und Stützenreaktionen. Ueber einer beliebigen Stütze r entsteht das negative max M_r, wenn die beiden anliegenden Oeffnungen vollbelastet sind und dann nach rechts und links unbelastete und vollbelastete Oeffnungen wechseln (Fig. 8), selbstverständlich soweit überhaupt die Oeffnungen reichen. Für das positive max M_r (oder negative min M_r) sind die beiden anliegenden Oeffnungen unbelastet und dann abwechselnd vollbelastete und unbelastete Oeffnungen anzunehmen (Fig. 8). Die zwei erwähnten Belastungen liefern auch die größte und kleinste Stützenreaktion R_r. In Fig. 9 sind beispielsweise die Belastungen für die Grenzwerte der Stützenmomente und Stützenreaktionen eines Trägers mit 4 Oeffnungen angedeutet.

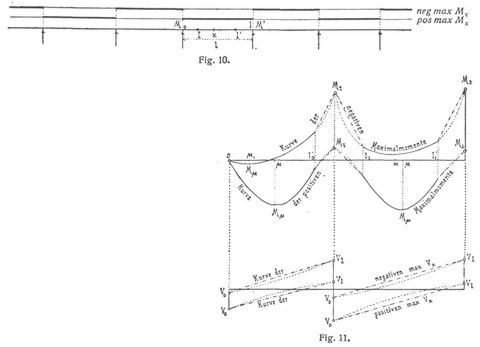
b) Momente zwischen den Inflexionspunkten. Die neg max M_x in allen Querschnitten x zwischen I und I' einer beliebigen Oeffnung l entstehen, wenn diese Oeffnung unbelastet ist und dann nach rechts und links belastete und unbelastete Oeffnungen wechseln (Fig. 10). Für die pos max M_x hat man die Oeffnung l vollbelastet und dann abwechselnd unbelastete und vollbelastete Oeffnungen anzunehmen (Fig. 10).

c) Uebrige Momente. Nach dem Bisherigen lassen sich sowohl die neg max M_x als die pos max M_x über den Stützen und zwischen den Inflexionspunkten aller Oeffnungen berechnen und die entsprechenden Teile der Kurven der neg max M_x und pos max M_x verzeichnen. In Fig. 11 ist dies für die 2 ersten Oeffnungen eines symmetrischen Trägers mit 4 Oeffnungen und frei drehbaren Enden geschehen, wobei die Punkte über den Stützen durch O angedeutet sind. Es fehlen dann noch die Grenzmomente zwischen den Inflexionspunkten und Stützen oder der Verlauf der Kurven der neg max M_x und pos max M_x daselbst. Für praktische Zwecke genügt es stets, diese fehlenden Kurvenstücke geradlinig, wie in Fig. 11 strichpunktiert, anzunehmen, womit man die Grenzwerte in den Zwischenpunkten etwas zu ungünstig erhält. Nähere Begründung und Beispiel der Berechnung in [10]. Den genauen Verlauf zeigen in Fig. 11 die einfach punktierten Linien. – Da bei kontinuierlichen Balken sowohl negative als positive Momente auftreten und damit beide Gurtungen sowohl Zug als Druck erhalten können, so sind abweichend vom einfachen Balken beiden Gurtungen für Zug und Druck geeignete Querschnitte zu geben.

d) Vertikalkräfte. In jeder Oeffnung l entsteht das neg max V_x bei x = 0, wenn die Oeffnung l und die nächstvorhergehende unbelastet sind und dann rechts und links vollbelastete[512] und unbelastete Oeffnungen wechseln (Fig. 12). Das neg max V_x bei x = l ergibt sich, wenn die Oeffnung l und die nächstfolgende vollbelastet sind und dann unbelastete und vollbelastete Oeffnungen wechseln (Fig. 13). Für die zwischen 0 und l liegenden Querschnitte x genügt es, die Linie der neg max V_x in der Oeffnung als eine Gerade anzusehen, sie also herzustellen, indem man neg max V₀ und neg max V_l bei 0 und l als Ordinaten anträgt und die Endpunkte der letzteren geradlinig verbindet (Fig. 11). In jeder Oeffnung l sind für das pos max V_x bei x = 0 die Oeffnung l und die nächstvorhergehende vollbelastet und dann abwechselnd unbelastete und vollbelastete Oeffnungen anzunehmen (Fig. 12). Das pos max V_x bei x = l entsteht, wenn die Oeffnung l und die nächstfolgende unbelastet sind, und dann rechts und links vollbelastete und unbelastete Oeffnungen wechseln (Fig. 13). Für die zwischen 0 und l liegenden Querschnitte x genügt es, die Kurve der pos max V_x als eine die Endpunkte der Ordinaten pos max V₀ und pos max V_l verbindende Gerade anzusehen (Fig. 11), wobei man wie im analogen Falle der neg max V_x die Grenzwerte etwas zu ungünstig erhält. Begründung und Beispiel der Berechnung in [10], genauer Verlauf der Kurven in Fig. 11 einfach punktiert. Anstatt die Grenzwerte der V_x in den Zwischenpunkten aus den Linien der max V_x zu entnehmen, kann man natürlich auch rechnen:

neg max V_x = (l – x)/l neg max V₀ + x/l neg max V_l,

39.

pos max V_x = (l – x)/l pos max V₀ + x/l pos max V_l.

40.

Tabellen zur Erleichterung der Berechnung für gleichmäßig verteilte Lasten s. [8], S. 223, 244, 264. Handelt es sich um bewegte Radlastzüge, so gilt bezüglich der Belastungen für die Grenzwerte alles soeben für gleichmäßig verteilte bewegte Last Gesagte, einschließlich der angeführten Ergänzungen der Kurven der max M_x und max V_x durch gerade Linien. Doch kommt noch in Frage, wie die Züge zusammenzustellen und welchen Punkten die Lasten möglichst zu nähern sind (s. Grenzwerte, Einflußlinien; Näheres [3], S. 42, 55, 61, 63, 144). Uebrigens wird auch bei kontinuierlichen Eisenbahnbrücken vielfach mit gleichmäßig verteilten Lasten gerechnet, die allerdings dann genügend hoch gerechnet werden müssen (vgl. Lastäquivalente).

Aenderung der Stützhöhen. Bezeichnet ∆ M_r die Aenderung des Stützenmoments M_r infolge aller Abweichungen der Stützpunkte (die in der Stabachse zu denken sind) von einer horizontalen oder geneigten Geraden, so stehen diese ∆ M für je drei aufeinanderfolgende Stützen in der Beziehung:

Mit den Aenderungen der Stützenmomente sind verbunden Aenderungen der Stützenreaktionen R_r um

und Aenderungen der Momente M_c und Vertikalkräfte V_x in allen Oeffnungen um

worin M, M' die Stützenmomente bei x = 0 und x = l bedeuten (Fig. 3, 10–13, und Balken, Fig. 1). In Fig. 14 ist angedeutet, welche Verschiebungen der Stützen negative Aenderungen von M_r und positive von R_r bedingen, für positive Aenderungen von M_r und negative von R_r wären die Pfeile umzukehren. Eine Aenderung der Stützenmomente und der von diesen abhängigen Beanspruchungen tritt nicht ein, wenn die Stützpunkte aus einer Geraden (z.B. I, Fig. 15) in eine andre Gerade (z.B. II, Fig. 15) geraten. Unbeabsichtigte Aenderungen der Stützhöhen sind also um so mehr zu fürchten, je nachgiebiger und ungleichmäßiger der Fundamentboden ist. Anderseits hat man aus dem Einfluß verschiedener Stützhöhen Vorteile zu ziehen gesucht. Vorgehen: Die Grenzwerte der Momente werden zunächst für Stützpunkte in einer [513] Geraden berechnet. Sodann ermittelt man nach 41. oder obigen Spezialformeln für die Stützenmomente symmetrischer Träger die nötigen Höhendifferenzen δ_r = c_{r + 1} – c_r unter den Bedingungen: 1. daß die negativen Maxima sämtlicher Stützenmomente gleich groß werden, 2. daß das größte positive Moment, das am Träger vorkommt, den größten negativen Momenten numerisch gleich werde. Bei Wahl dieser Stützhöhen wird das numerisch größte Moment am Träger überhaupt und damit im Falle konstanten Querschnitts der Materialverbrauch für die Gurtungen so klein als möglich. Es lassen sich bei kleinen bis mittleren Spannweiten Ersparnisse von 15–25% Gurtungsmaterial erreichen, doch wird man bei kleinen Spannweiten von Senkungen überhaupt absehen und bei größeren nur dann Gebrauch davon machen, wenn man sicher in, die berechneten Stützhöhen auch genau herstellen und dauernd erhalten zu können. Bei veränderlichen Gurtungsquerschnitten ist durch Aenderung der Stützhöhen überhaupt kein Vorteil erreichbar. Näheres mit Beispielen der Berechnung s. [3], S. 96, 112, 125, 148, 155.

Temperatureinflüsse. Ist auf irgend eine Art, z.B. weil der Untergurt vor unmittelbarer Einwirkung der Sonne geschützt war (s. Biegung I), eine Temperaturdifferenz t zwischen Oberkante und Unterkante des Balkens entstanden, so erleiden die Stützenmomente M_r Aenderungen ∆ M_r, die für drei aufeinander folgende Stützen in folgender Beziehung stehen:

Hierin bedeuten α den Ausdehnungskoeffizienten des Trägermaterials (für Schweißeisen etwa 0,000012, für Flußeisen und Stahl 0,0000115, s. Ausdehnungskoeffizient), h die Trägerhöhe. Die entsprechenden Aenderungen der Stützenreaktionen R_r, Momente M_x und Vertikalkräfte V_x sind durch 42.–44. bestimmt. – Der fragliche Einfluß machte sich zuerst bei kontinuierlichen Drehbrücken geltend, für welche daraus eine Erhöhung des Drucks auf die Endstützen resultiert, der bei Berechnung der Drehvorrichtung in Betracht zu ziehen ist. Für kontinuierliche Balken mit 2 Oeffnungen l₀, l₁ (Fig. 16) liefern die obigen allgemeinen Gleichungen die Aenderungen des Moments und der Reaktion der Mittelstütze:

der Reaktionen der Endstützen:

des Moments und der Vertikalkraft bei beliebigen x in l₀:

und derselben Größen in l₁:

Speziell für 2 gleichlange Oeffnungen l₀ = l₁ = l vereinfachen sich die Ausdrücke für die R in

Spezielleres über die Berechnung der Drehbrücken s. [13], 2. Bd., 4. Abt.

Literatur: [1] Clapeyron, Calcul d'une poutre élastique reposant librement sur des appuis inégalement espacés, Comptes rendus, 1857, XLV, p. 1076 (Wahl der Stützenmomente als statisch unbestimmter Größen). – [2] Mohr, Beitrag zur Theorie der Holz- und Eisenkonstruktionen, Zeitschr. des Architekten- u. Ingenieurvereins zu Hannover 1868, S. 19 (Graphische Bestimmung der Stützenmomente). – [3] Weyrauch, Allgem. Theorie und Berechnung der kontinuierlichen und einfachen Träger, Leipzig 1873. – [4] Laißle und Schübler, Der Bau der Brückenträger, Stuttgart 1876, Bd. 1, S. 161. – [5] Weyrauch, Temperatureinflüsse bei kontinuierlichen Trägern, Zeitschr. für Baukunde 1879, S. 437. – [6] Castigliano, Théorie de l'équilibre des systèmes élastiques, Turin 1880, p. 203 (auf Grund des Prinzips der kleinsten Verschiebungsarbeit). – [7] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 102, 104, 150. – [8] Winkler, Theorie der Brücken, Wien 1886, Heft I, S. 90. – [9] Weyrauch, Zur Vereinfachung der Berechnung durchgehender Träger, Zeitschr. des Architekten- u. Ingenieurvereins zu Hannover 1890. – [10] Toulon, Résistance des poutres droites à travées solidaires sur appuis élastiques, Comptes rendus, 1895, CXXI, p. 892. – [11] Müller-Breslau, Die graphische Statik der Baukonstruktionen, Bd. 2, Abt. 2, Leipzig 1896, S. 32. – [12] Dietz, Bewegliche Brücken, Leipzig 1897 (Fortschritte der Ingenieurwissenschaften, 2. Gruppe, 5. Heft). – [13] Handbuch der Ingenieurwissenschaften, 1901, 2. Bd., 2. Abt., S. 342. – [14] Vianello, Der durchgehende Träger auf elastisch senkbaren Stützen, Zeitschr. des Vereins deutscher Ingenieure 1904, S. 128, 161.

Weyrauch.

Balken, durchlaufende. (Graphische Berechnung.)

Die graphische Bestimmung der Auflagerdrücke, Querkräfte und Biegungsmomente eines durchlaufenden Balkens stützt sich auf das Verfahren zum Zeichnen der Biegungslinie. Kennt man die Kräfte, die auf einen Balkenträger einwirken, so zeichnet man zuerst mittels eines Seilpolygons (s.d.) dessen Momentenfläche, betrachtet sodann die Momentenfläche als Belastungsfläche (s. Seilkurve) und zeichnet dazu ein zweites Seilpolygon, wobei man die Polweite dem Trägheitsmomente (s.d.) des Balkenquerschnitts proportional macht. Dann stellt dieses zweite Seilpolygon die lotrecht verzerrte Biegungslinie (s.d.) des Balkens[514] dar. Das Maß der Verzerrung ist H a h: EJ, worin H die Polweite des ersten Seilpolygons, a die Verwandlungsbasis (s. Verwandlung von Flächen) der Belastungsfläche, h die Polweite des zweiten Seilpolygons, E den Elastizitätsmodul (s.d.) des Balkens und J das Trägheitsmoment des Balkenquerschnitts bedeutet. Liegen die Auflager des kontinuierlichen Balkens in einer geraden Linie, so hat das Verzerrungsverhältnis auf die Berechnung des Balkens keinen Einfluß. Bei ungleich hohen Stützpunkten sind deren Höhenunterschiede mit diesem Verhältnisse multipliziert in die Zeichnung einzuführen.

Das Trägheitsmoment wird in der Folge als konstant angenommen. Solange sich die Höhe des Balkens nicht ändert, was bei Balken mit mehr als 2 Oeffnungen meistens zutrifft, ist diese Annahme gestattet. Wechselnde Balkenhöhe kommt fast nur bei Balken mit 2 Oeffnungen (beispielsweise bei Drehbrücken) vor. – Die Berechnung solcher Balkenträger s. Fachwerk.

Bei der statischen Berechnung der kontinuierlichen Balken betrachtet man in der Regel nicht die Auflagerdrücke, sondern die Biegungsmomente über den Stützpunkten (Stützenmomente, Pfeilermomente) als die Unbekannten. Sind diese gefunden, so kann man die Momentenfläche zeichnen und mit ihrer Hilfe auch die Auflagerdrücke und Querkräfte finden.

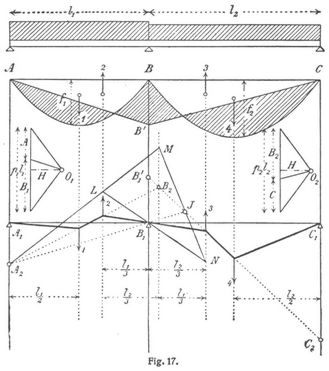
Balken mit 2 Oeffnungen. Der Balken A B C (Fig. 17) habe in der ersten Oeffnung die gleichförmig verteilte Last p₁l₁, in der zweiten die Last p₂l₂ zu tragen. Die Parabeln AB und BC stellen die Momentenflächen dar für den Fall, daß die Kontinuität über der Stütze B aufgehoben wird. Die zu diesen Parabeln gehörenden Kräftepolygone mit den Polen O₁ und O₂ sind unterhalb gezeichnet. Die Pfeilhöhen der Parabeln sind f₁ = (p₁l₁²)/(8H) und f₂ = (p₂l₂²)(8H). Die Polweite H wird beliebig gewählt. BB' sei das infolge der Kontinuität auftretende Stützenmoment. Dann stellt die schraffierte Fläche die Momentenfläche dar.

Wir zerlegen diese Fläche in zwei positive Parabelsegmente AB und BC und zwei negative Dreiecke ABB' und BB'C. Läßt man die Inhalte dieser vier Flächen in den jeweiligen Schwerpunkten als lotrechte Kräfte wirken und setzt diese Kräfte durch ein Seilpolygon zusammen, so bekommt man den Linienzug A₁ B₁ C₁. Dieses zweite Seilpolygon deckt sich zwar nicht mit der Biegungslinie des Balkens, fällt jedoch an den Auflagerstellen mit dieser zusammen. Die Punkte A₁, B₁ und C₁ müssen daher mit den Stützpunkten übereinstimmen.

Die Kräfte 1 und 4 liegen in den Mitten, die Kräfte 2 und 3 in den Dritteln der betreffenden Oeffnungen. Ferner liegt der Schnittpunkt B₂ der Seilpolygonseiten 1–2 und 3–4 auf einer lotrechten Linie, welche die Entfernung der Kräfte 2 und 3 im umgekehrten Verhältnisse ihrer Größe, also im Verhältnisse l₂ : l₁ teilt. (Vgl. Parallelkräfte.) Diese Linie wird »verschränkte Drittellinie« genannt. Man findet sie, wenn man von der Kraft 2 aus ¹/₃ l₂ nach rechts oder auch von der Kraft 3 aus ¹/₃ l₁ nach links aufträgt. Die Strecke A₁ A₂ ist das statische Moment der Kraft 1, C₁ C₂ das statische Moment der Kraft 4. (Vgl. Parallelkräfte.) Ist a die Verwandlungsbasis und h die zweite Polweite, so wird

und

Macht man, was sich am besten empfiehlt, ah = ¹/₆l₂² so wird einfacher

und C₁C₂ = 2f₂.

Auf Grund der bekannten Elemente läßt sich nun das Seilpolygon A₁ B₁ C₁ zeichnen. Zieht man zunächst von dem bekannten Punkte A₂ aus die Seilpolygonseite 1–2 in beliebiger Richtung, z.B. in der Richtung A₂ LM, zieht hierauf LB₁ N und verbindet M mit N, so schneidet die Linie A₂ B₁ auf M N den auf der Seilseite 3–4 liegenden Punkt J ab. Zieht man nämlich die Linie A₂ LM in verschiedenen Richtungen und zeichnet jeweils das Dreieck LMN, so bilden die verschiedenen Punkte L, M und N ähnliche Punktreihen und die Verbindungslinie MN geht stets durch den festen Punkt J. Ist J gefunden, so kann man die Seite 3–4 und von ihr aus alle übrigen Seiten des Seilpolygons ziehen. – C₂J schneide auf der B-Linie die Strecke B₁B₁' ab. Diese ist als statisches Moment der Kraft 3 gleich

oder da ah = ¹/₆l₂² [515] gemacht wurde, gleich BB', gleich dem gesuchten Stützenmomente. Um das Stützenmoment über B zu finden, zieht man somit die verschiedenen Drittellinien, trägt die Strecken A₁ A₂ und C₁ C₂ auf, bestimmt von A₂ aus mittels des Dreieckes LMN den Punkt J und zieht die Linie C₂JB₁'.

Legt man endlich durch den Pol O₁ eine Parallele zu AB' und durch den Pol O₂ eine Parallele zu B'C, so bekommt man die Auflagerdrücke A, B und C, wobei B = B₁ + B₂.

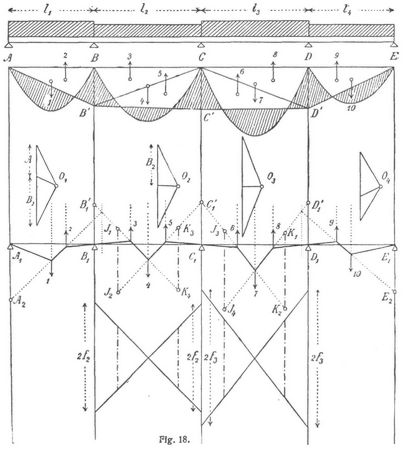
Balken mit mehr als 2 Oeffnungen. Das für 2 Oeffnungen abgeleitete Verfahren kann leicht auf mehr als 2 Oeffnungen ausgedehnt werden. Als Beispiel wählen wir einen Balken mit 4 Oeffnungen l₁, bis l₄ (Fig. 18). Der Einfachheit halber sei l₁ = l₄ und l₂ = l₃. Die vier Parabeln AB, BC, CD und DE seien bei aufgehobener Kontinuität die Seilpolygone für die gegebenen Belastungen, BB', CC' und DD' die zu bestimmenden Stützenmomente. Die schraffierte Fläche ist die Momentenfläche des Balkens. Wir zerlegen sie in vier positive Parabelsegmente und sechs negative Dreiecke, betrachten die Flächeninhalte dieser 10 Figuren als Kräfte und setzen sie durch ein Seilpolygon A₁ B₁ C₁ .... zusammen. Dann liegen wieder die Kräfte 1, 4, 7 und 10 in den Mittellinien, die Kräfte 2, 3, 5, 6, 8 und 9 in den Drittellinien der einzelnen Oeffnungen. Ferner schneiden sich 1–2 und 3–4 auf der verschränkten Drittellinie bei B₁, 4–5 und 6–7 auf der verschränkten Drittellinie bei C₁ u.s.w. Der Symmetrie wegen fällt die verschränkte Drittellinie bei C₁ mit der Auflagerlinie zusammen. A₁A₂ ist wiederum gleich 2f₁[(l₁)/(l₂)]² und E₁E₂ gleich 2f₄[(l₄)/(l₂)]², worin f₁ den Pfeil der ersten, f₄ den Pfeil der vierten Parabel bezeichnet. Unterhalb des zweiten Seilpolygons zeichnen wir ferner zwei Paare von sich kreuzenden Linien, die auf den Auflagerlinien die Strecken 2f₂ bezw. 2f₃ begrenzen. Diese Linien nennt man »Kreuzlinien«; sie schneiden auf jeder durch den Balken gelegten Vertikalen das statische Moment der Kraft 4, bezw. der Kraft 7 ab.

Nun findet man wie früher von A₂ aus mittels eines Dreieckes LMN den Punkt J₁ auf der Seilseite 3–4. Von J₁ aus trägt man eine Strecke J₁ J₂ auf, die man lotrecht darunter zwischen den Kreuzlinien abgreift. Hierauf bestimmt man von J₂ aus den Punkt J₃ gerade so, wie vorhin von A₂ aus J₁ bestimmt wurde, und trägt von J₃ aus den lotrecht darunter abgegriffenen Abschnitt J₃ J₄ auf. Die nämliche Arbeit führt man sodann, von E₂ ausgehend, in der Richtung von rechts nach links aus, wobei man die Punkte K₁, K₂, K₃ und K₄ erhält. Nun geht die Seilpolygonseite 3–4 durch J₁ und K₄, die Seite 4–5 durch J₂ und K₃, 6–7 durch J₃ und K₂, 7–8 durch J₄ und K₁. Durch kreuzweises Verbinden der Punkte J und K bekommt man somit vier Seiten des zweiten Seilpolygons und kann hiernach leicht das ganze Seilpolygon zeichnen. Zur Bestimmung der Stützenmomente ist letzteres nicht nötig, denn die Verbindungslinien der Punkte J und K schneiden diese Stützenmomente je über den Auflagerpunkten ab. Es ist B₁B₁' = BB', C₁C₁' = CC', D₁D₁' = DD'.

Ueberträgt man diese Abschnitte in die Momentenfigur, so gelangt man zu den Schlußlinien AB', B'C', C'D' und D'E und hiermit zur ganzen Momentenfläche. Zieht man endlich in den Kräftepolygonen Parallelen zu den Schlußlinien, so bekommt man auch die Auflagerdrücke.

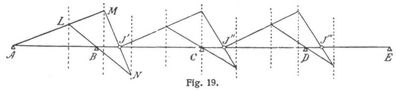
Sollen verschiedene Belastungsfälle behandelt werden, so ist es ratsam, die J- und K-Linien ein für allemal zu bestimmen. Hierzu dient die Fig. 19: Man trägt die verschiedenen Drittellinien auf und zeichnet, vom Punkte A ausgehend, das Dreieck L M N;[516] dadurch bekommt man den Punkt J' und zugleich die lotrechte Linie, auf der die Punkte J₁ und J₂ der Fig. 18 liegen. Von J' aus findet man in gleicher Weise den Punkt J'', der die Vertikale für J₃ und J₄ angibt. Schließlich wird auch noch der Punkt J''' bestimmt; letzterer gelangt erst später zur Verwendung. Durch symmetrische Uebertragung bekommt man die entsprechenden Punkte K. Die so bestimmten lotrechten Linien durch die J- und K-Punkte sind von der Belastung des Balkens unabhängig; sie heißen die »Fix–« oder »Festlinien«, auch »Inflexionslinien« des kontinuierlichen Balkens. Sind diese Linien bekannt, so genügt es, um J₁ (Fig. 18) zu finden, durch A₂ und B₁ eine Linie zu ziehen, bis sie die J-Linie schneidet. Ebenso findet man den Punkt J₃ dadurch, daß man J₂C₁ zieht und bis zur nächsten J-Linie verlängert.

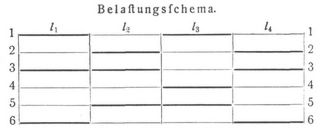
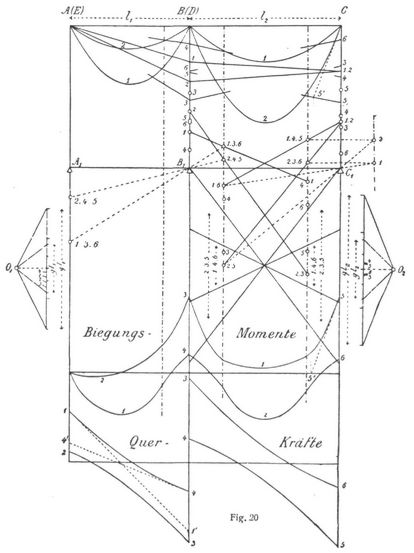
Kräfteplan eines Balkens mit 4 Oeffnungen. Die vollständige Berechnung eines durchlaufenden Balkens umfaßt gewöhnlich die Aufgabe, für gegebene Belastungen die Kurven der größten und kleinsten Biegungsmomente, sowie die Kurven der größten und kleinsten Querkräfte zu zeichnen. Für einen Balken mit 4 symmetrischen Oeffnungen sind sechs verschiedene Belastungsfälle hierzu nötig. In dem beigefügten Belastungsschema bedeutet ein schwacher Strich Belastung durch Eigengewicht (g auf die Längeneinheit), ein starker Strich volle Belastung (q auf die Längeneinheit). Der Belastungsfall 1 gibt für die erste und dritte Oeffnung die größten positiven, für die zweite und vierte Oeffnung die größten negativen Momente, der Belastungsfall 2 umgekehrt für die erste und dritte Oeffnung die größten negativen, für die zweite und vierte Oeffnung die größten positiven Momente. Durch den Fall 3 erhält man das größte negative, durch den Fall 4 das größte positive Moment am Pfeiler B, durch die Fälle 5 und 6 ebenso die größten Momente am Pfeiler C. Auch die größten und kleinsten an den Auflagern auftretenden Querkräfte werden durch diese sechs Belastungsfälle erhalten (vgl. Fig. 20). – Für jeden dieser Belastungsfälle wird nun die Konstruktion der Fig. 18 wiederholt. Dabei vereinigt man, um Platz und Arbeit zu ersparen, sämtliche Einzelfiguren in einer einzigen Zeichnung. Ueberdies ist es zweckmäßig, die rechte Hälfte der Zeichnung auf die linke herüberzuklappen. So gelangt man auf die Fig. 20. Sie enthält alle erforderlichen Linien[517] und Punkte. Die flachen Parabeln AB und BC entsprechen dem Eigengewicht, die neuen der vollen Belastung. Die beigeschriebenen Zahlen beziehen sich auf das Belastungsschema. Am unteren Ende der Figur sind die größten und kleinsten Momente sowie die größten und kleinsten Querkräfte von je einer gemeinschaftlichen Abszisse aus aufgetragen. Um die Momentenkurven zu erhalten, trägt man zunächst die Ordinaten der Momentenflächen 1 und 2 auf, wobei man die parabolischen, mit 1 und 2 bezeichneten Kurven erhält. Diese Kurven besitzen jedoch nur bis zu den strichpunktierten J- und K-Linien Gültigkeit. Von da zweigen die Momentenkurven ab und endigen am Auflager B in den Punkten 3 und 4, am Auflager C in den Punkten 5 und 6. Diese Abzweigungen werden nach dem Augenmaß eingezeichnet, wobei man zur Erzielung größerer Genauigkeit vorerst die Endtangenten zeichnen kann (vgl. die Tangente im Punkte 5). Um die Kurven der Querkräfte zu erhalten, bestimmt man in den Kräftepolygonen durch Parallelen zu den Schlußlinien die Auflagerdrücke und trägt diese unten von einer zweiten Abszisse aus auf. Dann bestimmt man in jedem Punkte die Tangente (vgl. 1–1' und 4–4')und zieht die verbindenden Kurven nach dem Augenmaß. Will man diese Kurven genauer erhalten, so muß man noch Fälle mit teilweiser Belastung der einzelnen Oeffnungen behandeln.

Einflußlinien. Mit dem bisher beschriebenen Verfahren reicht man bei der Berechnung von Straßenbrücken und Hochbauträgern meistens aus. Bei Eisenbahnbrücken wird auch der Einfluß des Eigengewichtes auf diesem Wege bestimmt. Zur Behandlung der Verkehrsart dagegen, die bei Bahnbrücken aus einer Reihe von Lokomotivachsen besteht, wendet man am besten Einflußlinien (s.d.) an. Die Lokomotivgewichte durch eine gleichwertige verteilte Belastung zu ersetzen, ist bei kontinuierlichen Brücken ein unsicheres Verfahren.

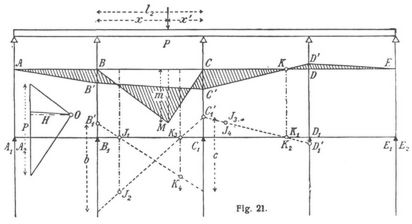
Um die Einflußlinien für Momente und Kräfte zu erhalten, müssen zunächst die Momentenflächen und Auflagerdrücke für eine Reihe von Einzellasten bestimmt werden. Fig. 21 stellt die Momentenfläche für eine in der zweiten Oeffnung befindliche Last P dar. Diese Fläche setzt sich aus einem positiven Dreieck BMC und den durch die Kontinuität entstehenden negativen Flächen zusammen. Das Dreieck BMC wird mittels des links davon aufgetragenen Kräftepolygons gezeichnet. Die Lage des Poles O wird dadurch gefunden, daß man die Last P umgekehrt proportional zu ihren Entfernungen von B und C in zwei Teile zerlegt und durch den Teilpunkt eine wagerechte Linie zieht. Die Polweite H wird nach Gutdünken angenommen.

Das Verfahren zur Bestimmung der Pfeilermomente für eine einzelne Last kann man ohne Schwierigkeit aus dem für verteilte Lasten entwickelten Verfahren ableiten. Läßt man in der Fig. 18 die Belastungen der ersten, dritten und vierten Oeffnung verschwinden, so verschwinden auch die positiven Momentenflächen dieser Oeffnungen. Infolgedessen werden die Kräfte 1, 7 und 10 und demgemäß auch die Strecken A₁ A₂, J₃ J₄, E₁ E₂ und K₁ K₂ gleich Null, und die Punkte A₂, J₁, E₂, K₁, K₂ und K₃ kommen sämtlich auf die wagerechte Linie A₁ E₁ zu liegen. Ferner fällt der Punkt J₄ mit J₃ zusammen. Demzufolge werden die Stützenmomente über C und D von der Doppellinie J_{3 ∙ 4}K_{1 ∙ 2} abgeschnitten. Dabei wird das Stützenmoment über D, abweichend von der gewöhnlichen Regel, positiv. Die Momente über C und D verhalten sich zueinander wie die Entfernungen der beiden Auflager von der K-Linie. Macht man in der Momentenfläche CC' = C₁C₁' und DD' = D₁D₁', so schneidet die Schlußlinie C'D' die Wagerechte im K-Punkte. Das Biegungsmoment in einem K-Punkte ist somit von der Belastung der links liegenden Oeffnungen unabhängig. Ebenso ist auch das Moment in einem J-Punkte von der Belastung der rechts liegenden Oeffnungen unabhängig.

Die Linien J₁K₄ und J₂K₃ sind nach früher die Seilpolygonseiten für das positive Dreieck BMC. Nennt man die Höhe des Dreiecks m und den Abstand seines Schwerpunktes von der B-Linie s, so ist der Abschnitt b, als statisches Moment betrachtet, gleich

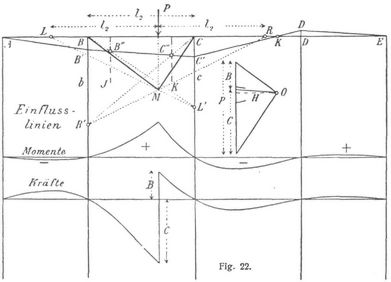
oder, wenn man s = ¹/₃ (l₂ + x) und wie früher ah = ¹/₆l₂² setzt, b = [(l₂ + x)/l₂]m. Ebenso wird c = [(l₂ + x')/l₂]m. Die Zeichnung der Momentenfläche für die Last P läßt sich nun wie folgt vereinfachen. Um b und c zu finden, trägt man (Fig. 22) die Spannweite l₂ von der Laststelle aus nach links und rechts auf und zieht die Linien LML' und RMR'. Dann ist BR' = b und CL' = c. Ferner sind BL' und CR' die Kreuzlinien für das Dreieck BMC. Verbindet man noch den Punkt B'', in dem BL' die J-Linie schneidet, mit dem Punkte C'', in dem CR' die K-Linie trifft, so bekommt man, wie ein Vergleich mit der Fig. 21 zeigt, in BB' und CC' die Stützenmomente und in B'C' die Schlußlinie. Die Linien B'A, C'KD' und D'E vervollständigen die Momentenfläche. Vier [518] Strahlen durch O, parallel zu den Linien AB', B'C', C'D' und D'E, bestimmen die Querkräfte für Schnitte links und rechts von der Last (B und C), sowie für Schnitte in der ersten, dritten und vierten Oeffnung.

Um nun die Einflußlinien für Momente und Kräfte zu erhalten, wiederholt man die soeben beschriebene Zeichnung für mehrere (10–15) über die erste und zweite Oeffnung verteilte Einzellasten. Man wählt hierzu am besten diejenige Last, die in der vorgeschriebenen Lastenreihe am häufigsten vorkommt. Dabei können die einzelnen Momentenflächen ganz gut in einer einzigen Zeichnung vereinigt werden.

Trägt man sodann die Momentenordinaten, die sich für ein und denselben Schnitt ergeben, von einer Abszisse aus jeweils lotrecht unter der betreffenden Last auf und verbindet deren Endpunkte, so erhält man die Einflußlinie für die Momente dieses Schnittes. In Fig. 22 ist diese Einflußlinie für den Schnitt M gezeichnet. Man erkennt, daß das Biegungsmoment für die in der zweiten und vierten Oeffnung liegenden Lasten positiv, für Lasten in der ersten und dritten Oeffnung dagegen negativ wird. Die ungünstigste Belastung für den Schnitt M erstreckt sich somit über die zweite und vierte, bezw. über die erste und dritte Oeffnung, vorausgesetzt, daß getrennte Verkehrslasten (Zugstrennungen) überhaupt zulässig sind. Wie man mit Hilfe dieser Einflußlinien die größten und kleinsten Momente findet, s. Einflußlinien.

Am Fuße der Fig. 22 ist auch die Einflußlinie für die Querkräfte des Schnittes M gezeichnet. Sie ergibt sich dadurch, daß man in den Kräftepolygonen der verschiedenen Einzellasten die Querkräfte abgreift und den Laststellungen entsprechend von einer Abszisse aus aufträgt. Die ungünstigste Belastung erstreckt sich für abwärts gerichtete Querkräfte von B bis zum Schnitte M, für aufwärts gerichtete Kräfte von C bis M. Unter Umständen sind auch noch die benachbarten Oeffnungen zu belasten. Es sei noch bemerkt, daß, während man bei den Momenten für jeden Schnitt eine besondere Einflußlinie zu zeichnen hat, die Einflußlinien für die Kräfte innerhalb einer Oeffnung stets zusammenfallen.

Literatur: Stelzel, Grundzüge der graph. Statik und deren Anwendung a. d. kontin. Träger, Graz 1882; Ritter, W., Die elastische Linie und ihre Anwendung a. d. kontin. Balken, Zürich 1883; Müller-Breslau, Wochenblatt für Archit. und Ing. 1883, S. 353; Winkler, E., Theorie der Brücken, Wien 1886, 1. Heft; Handbuch der Ingenieurwissenschaften, Leipzig 1889–90, Bd. 2, 2. Abteil.; Land, R., Zeitschr. f. Bauwesen 1890, S. 106; Ritter, W., Anwendungen der graph. Statik, III. Teil: Der kontinuierliche Balken, Zürich 1900.

(W. Ritter) Roth.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4., Fig. 5.

Fig. 6.

Fig. 7.

Fig. 8.

Fig. 9.

Fig. 10., Fig. 11.

Fig. 12.

Fig. 13.

Fig. 14., Fig. 15.

Fig. 16.

Fig. 17.

Fig. 18.

Fig. 19.

Fig. 20.

Fig. 21.

Fig. 22.