- Massenmittelpunkt
Massenmittelpunkt (Schwerpunkt) ist jener Punkt S eines Massensystems, in welchem die in ihm vereinigte Gesamtmasse des Systems gleiches polares Moment ersten Grades in bezug auf jeden Punkt und jede Ebene hat wie das Massensystem selbst. Es geht durch ihn insbesondere stets die Resultante von Parallelkräften, die den Massen proportional sind und in ihnen angreifen, z.B. von Schwerkräften.
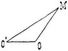
Das Produkt m · O M aus der Masse m eines Punktes M und dessen Abstand O M von einem Punkte O heißt das polare Moment ersten Grades der Masse m in bezug auf den Punkt O. Es ist das m fache der Strecke O M und wird selbst durch eine von O ausgehende Strecke von der Richtung und dem Sinne von O M oder M O dargestellt. Die geometrische Summe oder Resultante der polaren Momente ersten Grades der Massenpunkte eines Systems in bezug auf einen Punkt O heißt das polare Moment ersten Grades dieses Massenpunktsystems in bezug auf O. Es ist die Schlußlinie O R eines von O aus mit den polaren Momenten m · O M der Punkte des Systems in beliebiger Folge konstruierten Polygons. Ist M die Gesamtmasse des Systems, so kann auf der Richtung von O R ein Punkt S gefunden werden, so daß M · O S = O R, d.h. daß das polare Moment ersten Grades des Punktes S, wenn in ihm die Gesamtmasse M vereinigt gedacht wird, in bezug auf O dem Momente des Systems gleich wird. Dieser Punkt S, dessen Moment ersten Grades in bezug auf jeden Punkt O gleich dem Moment des Systems in bezug auf denselben Punkt ist, heißt der Massenmittelpunkt des Systems. Die Lage dieses Punktes S im System hängt von dessen Konfiguration und Massenverteilung, nicht aber von der Lage des Punktes O ab. Bildet man nämlich für zwei Punkte O, O' die Momente, so ist M · [O' S'] = Σm [O' M], M · [O S] = Σm [O M], wo S' für O' dieselbe Bedeutung hat, wie S für O und die Klammern andeuten sollen, daß die Strecken Größen von bestimmter Richtung[320] und bestimmtem Sinne sind. Daher wird M([O' S'] – [O S]) = Σm([O' M] – [O M]). Nun ist aber (s. die Figur) [O' M] – [O M] = [O' O] und daher die rechte Seite dieser Gleichung gleich Σm[O' O] = [O' O]Σm = M · [O' O] und folglich [O' S'] – [O S] = [O' O], d.h. [O' S'] = [O' O] + [O S] = [O' S], d.h. es ist O' S' geometrisch, d.h. nach Größe, Richtung und Sinn gleich O' S und fällt daher S' mit S zusammen.
Projiziert man das Polygon auf irgendeine Achse, z.B. auf die x-Achse eines Koordinatensystems der x, y, z, so ist die Projektion der Schlußlinie M · O S gleich der Summe der Projektionen der Seiten m · O M. Sind also x, y, z die Koordinaten des Systempunktes M, x0, y0, z0 die des Poles O und x1, y1, z1 die des Massenmittelpunktes S, so sind x – x0 und x1 – x0 die Projektionen von O M und O S und daher M(x1 – x0) = Σm(x – x0), oder da M x0 = Σ m x0 ist, Mx1 = Σ m x und ebenso für die beiden andern Achsen My1 = Σ m y, Mz1 = Σ m z. Da x und x1 die Abstände der Punkte M und S von der y z-Ebene sind und diese eine beliebige Ebene ist, so sagt die erste dieser Gleichungen aus, wenn man das Produkt m x aus der Masse m eines Punktes und seines Abstandes von einer Ebene das Moment ersten Grades desselben in bezug auf die Ebene nennt, daß die Summe der Momente ersten Grades aller Systempunkte in bezug auf jede Ebene gleich dem Momente des Massenmittelpunktes in bezug auf dieselbe Ebene ist, wenn man ihm die Gesamtmasse M des Systems als Masse zu erteilt. Geht die Ebene durch den Massenmittelpunkt, so ist das Moment in bezug auf sie Null und umgekehrt. Aus diesen Betrachtungen ergeben sich die Sätze: 1. Das polare Moment ersten Grades eines Massenpunktsystems ist konstant für alle Punkte einer um den Massenmittelpunkt beschriebenen Kugelfläche, es kann jeden Wert von 0 bis ∞ erreichen und verschwindet im Massenmittelpunkt als Pol; 2. der Massenmittelpunkt eines ebenen Systems fällt in die Ebene, der eines geradlinigen Systems in die Gerade desselben; 3. projiziert man ein System auf eine Ebene oder eine Gerade und erteilt den Projektionspunkten dieselbe Masse wie den Hauptpunkten, so ist die Projektion des Massenmittelpunkts der Massenmittelpunkt der Projektion des Systems; 4. haben die Massenpunkte paarweise gleiche Massen, welche symmetrisch gegen eine Ebene liegen, so liegt der Massenmittelpunkt in dieser Ebene; gibt es zwei oder drei solcher Ebenen, so liegt er in deren Durchschnittslinie oder ihrem Schnittpunkt; 5. dasselbe gilt von Diametralebenen, d.h. von Ebenen, welche ein System von Parallelstrecken halbieren, welche Punkte gleicher Masse paarweise verbinden; 6. hat das System eine Symmetrieachse, d.h. eine. Gerade, welche die Verbindungslinien paarweise gleicher Massen halbiert, so liegt der Massenmittelpunkt in ihr; 7. hat das System einen Mittelpunkt, in welchem sich die Verbindungslinien paarweise gleicher Massen schneiden, so ist er der Massenmittelpunkt; 8. zerlegt man das System in Partialsysteme, sucht deren Massenmittelpunkte auf und erteilt diesen die Masse der Partialsysteme, so ist der Massenmittelpunkt des Gesamtsystems der Massenmittelpunkt dieser Massenmittelpunkte.
Diese Sätze dienen zur Bestimmung des Massenmittelpunktes der Systeme, sowohl der aus diskreten Punkten bestehenden als auch der kontinuierlichen. Die anzuwendenden Methoden sind teils rein geometrischer Natur, teils sind sie Methoden der Integralrechnung. Die kontinuierlichen Systeme sind Massenpunktlinien, Massenpunktflächen und körperliche Räume mit Masse erfüllt. Ein Punkt einer Massenlinie ist als ein verschwindendes Linienelement, ein Punkt einer Mattenfläche als Flächenelement, ein Punkt eines Massenraumes als körperliches Element anzusehen. Sind x, y, z die Koordinaten eines solchen Punktes und d m das in ihm enthaltene Massenelement sowie x1, y1, z1 die Koordinaten des Massenmittelpunktes, in welchem die Gesamtmasse m vereinigt gedacht wird, so bestehen für kontinuierliche Systeme die Gleichungen: m x1 = ∫ x d m, m y1 – ∫ y d m, m z1 = ∫ z d m, worin das Integralzeichen ein einfaches, doppeltes oder dreifaches Integral darstellt, je nach der linien- oder flächenartigen oder körperlichen Beschaffenheit des Systems, ausgedehnt über dessen ganze Masse. Bedeutet ρ die spezifische Masse des Elementes d m, wo ρ eine Funktion der Koordinaten x, y, z sein wird, so wird d m = ρ d s, d m = ρ d ω, d s = ρ d ω, wenn d s, d ω, d v das Linienelement, Flächen- oder Volumenelement darstellt. An die Stelle der x, y, z können natürlich auch andre Koordinaten treten, je nach der Wahl der analytischen Darstellung der Punkte, Linien oder Flächen. Der Massenmittelpunkt ist zugleich auch der Mittelpunkt paralleler Schwerkräfte und Angriffspunkt des Gesamtgewichtes eines schweren Systems. Er heißt daher auch der Schwerpunkt eines solchen. Ist das System homogen, also ρ konstant, so wird m das Produkt aus ρ und der Länge s der Linie oder dem Inhalt ω der Fläche oder dem Volumen v des Körpers und fällt ρ aus den Gleichungen für x1, y1, z1 heraus, so daß diese die Form annehmen s x1 = ∫ x d s, s y1 = ∫ y d s, s z1 = ∫ z d s; ω x1 = ∫ x d ω, ω y1 = ∫ y d ω, z ω = ∫ z d ω; v x1 = ∫ x d v, v y1 = ∫ y d v, v z1 = ∫ z d v. Zur Bestimmung der Koordinaten des Massenmittelpunktes ist auch die Bestimmung der Masse notwendig. Sie ist durch m = ∫ ρ d s, m = ∫ ρ d ω, m = ∫ ρ d v gegeben, je nach der linien- oder flächenartigen oder körperlichen Verteilung der Massenpunkte. Für homogene Systeme wird die Masse durch die Bogenlänge, den Flächeninhalt und das Volumen vertreten.
Schon Archimedes hat Massenmittelpunkte homogener Figuren bestimmt; zwei Sätze über den Massenmittelpunkt rühren von Pappus her und finden sich in dessen Collectiones mathematicae, lib. VII, werden aber gewöhnlich Guldin (1577–1663) zugeschrieben, der sie in seinen Werken »De centro gravitatis« (1635) und »Centrobaryca« (1643) reproduzierte (vgl. Guldinsche Regeln). Graßmann hat die Lehre vom Massenmittelpunkt als eine eigenartige Punktrechnung ausgebildet (vgl. hierüber die Schrift seines Sohnes H. Graßmann, Punktrechnung und projektive Geometrie, 1. Teil, in der Festschrift der lateinischen Hauptschule zur zweihundert jährigen Jubelfeier der Universität Halle-Wittenberg). Die Werke über Mechanik enthalten meistens ausgedehnte Abschnitte über die Bestimmung des Massenmittelpunktes oder Schwerpunktes, insbesondere seien hier erwähnt: Poinsot, Elements de statique, 11. édit. par Bertrand, Paris 1873, S. 142–174; Möbius, Lehrbuch der Statik, 1. Teil, S. 110–113, oder Gesammelte Werke, Bd. 3;[321] Routh, A treatise on analytic statics, Cambridge 1891, Bd. 1, S. 270–314; Schell, Theorie der Bewegung und der Kräfte, Leipzig 1879, Bd. 1, S. 72–100; sowie die Sammlungen von Aufgaben: Jullien, Problèmes de mécanique rationelle, 2. édit., Paris 1866, 1. Teil, S. 1–42; Walton, Collection of problems in illustration of the principles of theoretical mechanics, Cambridge 1855, S. 1–39; Kraft, Sammlung von Problemen der analytischen Mechanik, Stuttgart 1885, Bd. 1, S. 527–607.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.