Dampfkolben

Dampfkolben für Dampfmaschinen (s.d. und Dampfzylinder) und für Dampfhämmer (s.d.) bestehen aus dem scheibenförmigen Kolbenkörper, der mit geringem Spielraum in den Zylinder paßt und mit seiner Nabe auf der Kolbenstange befestigt ist, und den Liderungsringen, die mit sanftem Druck dicht an der Zylinderwand anliegen und gleiten. Das Gewicht des Kolbens wird bei liegenden Maschinen schwebend von der Kolbenstange getragen, die ihrerseits in den Stopfbüchsen und Führungen aufliegt, oder es ist auf den Dichtungsringen federnd gestützt oder wird auch unmittelbar vom Zylinder aufgenommen; bei stehenden Maschinen ruht der Kolben nur auf der Kolbenstange, so daß die Abnutzung des Zylinders gleichmäßig erfolgt.

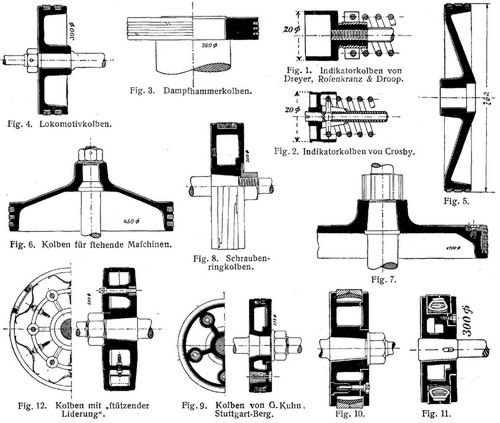
[589] Allgemeines. Fig. 1 und 2: Kolben ohne Liderungsringe für Indikatoren, auch für kleine schnellaufende Maschinen, werden im Zylinder passend eingeschliffen und dichten am Umfang mit mehreren seinen Rillen, die sich mit Wasser und Oel füllen. – Fig. 3: Massiver Kolben für Dampfhämmer mit drei Stahlringen von fast quadratischem Querschnitt mit 6–12 mm Stärke. – Fig. 4: Lokomotivkolben, aus Schmiedeeisen gepreßt oder aus Stahl gegossen, mit gußeisernen selbstspannenden Ringen, die über die Ränder des Kolbenkörpers in die Nuten geschoben werden. – Fig. 5: Lokomotivkolben amerikanischer Bauart, mit kegelförmiger Scheibe, der am Umfang mit einem das Gewicht im Zylinder tragenden Laufring von Weißmetall ausgegossen ist. – Fig. 6: Kolben für stehende Maschinen mit Trichterform zur Erhöhung der Widerstandsfähigkeit und zur Abführung des Wassers nach außen, mit drei übergeschobenen Selbstspannringen. – Fig. 7: Desgleichen mit flacher Scheibe und besonderem, auswechselbarem Kranz für die Ringnuten. – Fig. 8: Hohlgußkolben mit einem schraubenförmig aus einem Gußzylinder gefrästen und zusammengedrückten Ringe, der vermöge seiner Federwirkung auch an den Stirnflächen der Nut dauernd dicht anliegt. – Fig. 9: Rippengußkolben mit aufgeschraubter Deckelscheibe, mit zwei Ringen und einer Zwischenlage, die sich leicht aufbringen lassen, auch durch Auswechslung der letzteren gegen eine stärkere wiederholt in die Kolbennut eingepaßt werden können, wenn sie in axialer Richtung lose geworden sind. – Fig. 10: Kolben mit Deckelscheibe und zwei Ringen von keilförmigem Querschnitt mit dahinterliegendem Spannring von Guß oder Stahl. – Fig. 11: Hohlgußkolben mit Deckelring und Spannfeder von doppeltem Stahldraht. – Unter »Dampfzylinder Fig. 3« ist ein Kolben dargestellt, dessen Ringe durch einzelne Rotgußkeilstücke mit darunterliegenden Blattfedern gespannt werden. – Fig. 12: Rippengußkolben mit sechs nachstellbaren Blattfedern innerhalb der beiden Dichtungsringe

Fig. 1–12 zeigen verschiedene Arten der Befestigung auf der Kolbenstange. Bei kleinen Kolben (bis 400 mm) kann der Deckel durch die Mutter der Stange am Kolbenkörper festgehalten werden. Besser und gebräuchlicher sind Kopfschrauben mit Muttern aus Rotguß; letztere sind rund von außen eingesetzt oder quadratisch in Aussparungen innerhalb des Kolbens eingeschoben. Die Schrauben werden in die Kolbenoberfläche eingelassen, damit sie nicht am Zylinderboden anstoßen und auch keine besonderen Aussparungen an diesem erfordern. Die Anzahl der Kolbenschrauben Z = 0,1D cm (+ 1) wird gewöhnlich auf eine gerade Zahl abgerundet; ihre Stärke kann zu d cm = 0,6∛D cm angenommen werden. Alle Verschraubungen am Kolben sind zu sichern. Zum Einsetzen von Abpreßschrauben im Deckel, der an seiner zylindrischen Anlagefläche festbrennt, versieht man ihn mit drei Bohrungen mit Muttergewinde, die im Betriebe durch Bronzeschrauben geschlossen gehalten werden.

[590] Der Kolbenkörper wird beansprucht durch den Dampfüberdruck, ferner durch die Beschleunigungskraft seiner Masse, wofür sich wieder ein gleichmäßiger Ueberdruck rechnen läßt, und durch die Reibung der Ringe am Umfang; dagegen wird er durch die Kolbenstange in seiner Mitte gestützt.

Eine ebene Scheibe mit Dem äußerem und D_n cm Nabendurchmesser und dem Verhältnis ∆ = D_n/D, als Platte (s.d.) von gleichmäßiger Wandstärke h für einen Gesamtüberdruck von q Atmosphären berechnet, erfordert h₀ = 0,35D√(q∆s) bei der Biegungsspannung s, die für Gußeisen 250–300 kg/qcm beträgt, für Stahlguß 400–600. Bei ungleicher Stärke der Scheibe kann 1,2 h₀ bis 1,3 h₀ an der Nabe und 0,8 h₀ bis 0,9 h₀ für den Umfang der Scheibe gesetzt werden. – In der Berechnung von Reymann [1] wird die Beanspruchung einer radialen Lamelle von einem kleinen Zentriwinkel ω untersucht. Zur Vereinfachung der Rechnung ist angenommen, daß das Trägheitsmoment des Lamellenquerschnittes konstant sei, daß also die Wandstärke w umgekehrt proportional der dritten Wurzel aus dem Radius nach außen abnimmt. Die größte Beanspruchung der Platte findet dabei am Nabenumfang statt. Die Wandstärke an dieser Stelle ergibt sich zu

Am äußeren Umfang ist

Dabei wird die Spannung s_a außen nur 0,3–0,4mal so groß als die Spannung s_n am Nabenumfang. Für einen Lokomotivkolben ist s_n = 633 und s_a = 240 kg/qcm berechnet, dazu die Ringspannungen in den Stirnflächen der Nabe von der Bohrung D₀ und der Höhe H zu 1,7 s_n h_n/H[1 – (D₀/Dn)²] = 782 kg/qcm. – Wenn man die Kolbenscheibe von gleichmäßiger Wandstärke in einfacher Weise so rechnet, als ob sie längs eines Durchmessers gestützt sei, während jede Hälfte gleichmäßig mit q Atmosphären beladet ist, so ergibt sich die Wandstärke zu

Das ist für große Kolben zu wenig.

Ein Hohlkolben ohne Rippen müßte in jeder Scheibe das 0,7fache der für die einfache Scheibe berechneten Stärke erhalten. Die Rippen versteifen die Scheiben gegenseitig; hierfür setzt Reymann [1] das Widerstandsmoment so an, als ob die Scheiben die Gurte radialer Träger bildeten, deren Stege indes unberücksichtigt bleiben. Für die ganze Kolbenhöhe H und die lichte Höhe H₁ ergibt sich dabei die Spannung in der Nähe der Nabe zu s_n = 0,25 q D² h (2 + ∆) (1 – ∆)²∆ (H³ – H₁³) wobei wieder ∆ = D_n/D ist. Die Ringspannung in der Nabe wird ähnlich wie vorher angegeben zu k = 1,7 s_n [1 – (H₁/H)²]/[1 – (D₀/D_n)²]. Beispielsweise findet sich s_n = 263 und k = 335 kg/qcm.

Der Trichterkolben stützt die radialen Lamellen durch die Ringspannungen der kegelförmigen Wandung so ab, daß infolge der Deformation unter der Belastung von außen ein Kegel von etwas spitzerem Winkel, jedoch wieder mit geraden Mantellinien entstehen würde. Die Biegungsmomente verschwinden. Es bleiben Zugspannungen s in Richtung der Mantellinien und Druckspannungen t in tangentialer Richtung. Nach der kurzen Entwicklung Reymanns [1] beträgt für q Atmosphären Dampfüberdruck und q₀ kg für je 1 qcm Zylinderquerschnitt als Wirkung des Massenwiderstandes bei Beschleunigung und des Eigengewichtes des Kolbens, in einem beliebigen Durchmesser d die Zugspannung s = (q + q₀)(D₂ – d²)/4dwsinα. Hierin bedeutet D den Kolbendurchmesser, w die Wandstärke und α den Winkel, den die Mantellinie mit dem Radius bildet; q und q₀ sind bald positiv, bald negativ wirksam. Die tangentiale Ringspannung ist t = (q + q₀ cos² α) d/2 w sin α. Für sehr kleine Winkel α, also für sehr flache Kegelflächen, hätte man den Nenner des vorigen Ausdruckes noch mit [1 + (w cos² α/R sin α)²] zu multiplizieren, um etwas weitere Annäherung zu erreichen. Dieser Zusatz findet sich, wenn man die Berechnung weiter verfolgt und dabei mehrfache Abkürzungen zuläßt. Für einen Stahlgußkolben ist für q = 5 Atmosphären die größte Zugspannung (an der Nabe) zu s = 404, die größte Ringspannung (am Umfang) zu t = 243 kg/qcm berechnet. Für Gußeisen kann 5 = 100–150 kg/qcm gesetzt werden; t wird kleiner als 5. Bei der üblichen Größe und Bauart der Trichterkolben kommt aber die eigentliche Kegelfläche kaum zur Geltung, weil die Deformationen und damit die Beanspruchungen vorwiegend nur noch durch die Grenzbedingungen der Biegungsmomente an der Nabe und am Bordrande beeinflußt werden, die bei der Durchführung der Theorie als Integrationskonstanten auftreten. Mit Rücksicht hierauf kommt man zu einer einfachen Näherungsmethode, wenn man den Trichterkolben wie einen ebenen Kolben behandelt, dessen Scheibe man sich in unendlich viele zylindrische Lamellen je von der Scheibenhöhe h und der Dicke d r geteilt und axial in die Trichterform verschoben denkt. Nach dieser Vorstellung bekäme der Trichterkolben in axialer Richtung die für den Scheibenkolben berechnete Stärke h, also eine senkrecht zur Kegelfläche gemessene Dicke w = h cos α. Eine Gewichtsersparnis tritt hierbei nicht ein, wenn man die Spannung nicht höher ansetzt.

Wenn ein Kolben einer liegenden Maschine im Zylinder unmittelbar aufliegt, soll der Flächendruck, berechnet aus dem Kolbengewicht auf die Breite von D cos 30° und die Länge H des Kolbens abzüglich der Ringe, höchstens ¹/_2#150;³/₄ kg/qcm betragen. Das erfordert eine Kolbenhöhe von etwa 0,25D + 5 cm und ¹/_2#150;1 mm exzentrische Kolbenlage.

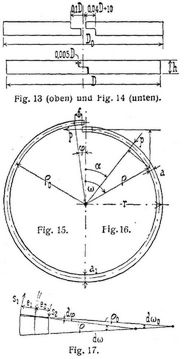
Die Kolbenringe werden von zähem Gußeisen hergestellt, das nicht weicher als das des Zylinders zu nehmen ist. Jeder Ring wird an einer Stelle des Umfanges aufgeschlitzt, damit er sich der Zylinderwand anpassen kann, und zwar entweder geradlinig in schräger Richtung oder mit gerader Ueberblattung (Fig. 14). Den Eintritt des Dampfes in die Fuge verhindert ein Metallblättchen, das an dem einen Ringende mit zwei versenkten Schrauben befestigt wird.

Liderungsringe, die durch innenliegende Federn oder Federringe gespannt gehalten werden, erhalten eine gleichmäßige Wandstärke a₀ = 0,033 D und eine Höhe h = 1,5 a₀, oder auch quadratischen oder trapezförmigen Querschnitt (Fig. 10 und 11).

Federringe oder Selbstspanner legen sich mit eigner Federkraft an die Zylinderwand,[591] indem sie von vornherein einen größeren Durchmesser erhalten. Man gießt dazu einen Hohlzylinder von der gewünschten Ringstärke, unter Zugabe von 3–6 mm zum Abdrehen auf den Außendurchmesser 1,04 D, mit der sechsfachen Ringhöhe, so daß man zwei Paar Kolbenringe abstechen kann, davon ein Paar zur Reserve, während das obere Ende als verlorener Kopf abfällt. Zweckmäßig wird der Ring auch innen ausgedreht; der Innenkreis liegt soviel exzentrisch, daß die Ringstärke an einer Stelle a₁ und an der gegenüberliegenden Stelle 0,7 a₁ wird. Die einzelnen Ringe werden an der dünnen Stelle aufgeschlitzt oder so ausgestoßen (Fig. 13), daß die Enden übereinander greifen können. Man heftet die Enden in der Lage Fig. 14 durch einen dünnen Stift in axialer Bohrung zusammen und dreht ihn so auf den Durchmesser D außen fertig. Die Stirnflächen werden mit Schmirgel und Oel passend zur Höhe der Ringnuten im Kolbenkörper geschliffen, so daß sie sich durch einen Stoß mit dem Hammerstiel gerade darin verschieben lassen. Hierbei wird der Ring, nach Entfernung des Heftstiftes, durch einen Bandeisengürtel zusammengespannt gehalten.

Der so hergestellte Ring legt sich im Zylinder mit ringsum gleichmäßigem Flächendruck an. Das Biegungsmoment für einen beliebigen, um den Winkel ω von der Teilstelle entfernten Querschnitt (Fig. 16), unter der Wirkung der vom Heftstift vermittelten Spannkraft P der beiden Enden, ist M = P r (1 – cos ω). Unter einem gleichmäßig von außen auf den Ring wirkenden Flächendruck p ist

Beide Kraftwirkungen geben also gleiche Momente für die einzelnen Querschnitte, mit P= phr, so daß die am zusammengehefteten Ringe auf der Drehbank hergestellte Kreisform auch im Zylinder wieder eintritt, wenn der Flächendruck gleichmäßig wirkt. Läßt man aber den Ring sich frei öffnen, so werden doch die Enden des Ringes außen den Radius r nahezu beibehalten. Der Krümmungsradius ρ₀ des offenen Ringes, Fig. 15, ist demnach nicht konstant, wohl aber der Krümmungsradius ρ der infolge Durchbiegung des Ringendes um das Maß f entstehenden elastischen Linie, Fig. 16.

Ein Bogenelement des Ringes, Fig. 17, vom Radius ρ₀ und Winkel d ω₀ verbiegt sich um d φ zu einem Bogen vom Radius ρ und Winkel d ω. Dabei bleibt die Länge ρ₀ d ω₀ = ρ d ω und es ist d ω = d φ + d ω₀, folglich d φ = (1/ρ – 1ρ₀) ρ d ω. Nach der allgemeinen Biegungsformel ist 1/ρ – 1/ρ₀ = M/E J; hierin hat man M = p h r² (1 – cos ω) einzusetzen, ferner 800000 kg/qcm für zähes Gußeisen und J = a³ h/12. Die Ringstärke a kann bei der Verjüngung von a₁ auf 0,7 a₁ zu a = a₁ [0,7 + 0,15 (1 – cos ω)] gerechnet werden. Die Annäherung d f des Ringendes an die Mittellinie, infolge der Krümmung d φ eines Bogenelementes im Abstande ρ (1 – cos ω) in Richtung der Mittellinie, beträgt d f = ρ (1 – cos ω) d φ. Ueber die genauere Entwicklung nach Grashof s. [2]. Aus den vorstehenden Aufteilungen folgt

Das Integral hat den Wert 5,6; man findet ihn leicht, indem man für 0° 30° ... 180° die Einzelwerte aufzeichnet, die Fläche unter der so bestimmten Kurve planimetriert, ferner die Einzelwerte von (1 – cos ω), deren Integral = π ist, ebenso behandelt und nach diesem Maßstabverhältnis den Gesamtwert feststellt. Mit ρ = rund 0,975 r und r = D/2 folgt a₁³ f = 4 p D⁴/E.

Man wählt gewöhnlich, wie in Fig. 13 und 14 angegeben ist, das Maß der Zusammenbiegung beider Ringenden 2 f = 0,1 D – 0,005 D oder f = 0,0475 D. Dabei ist der mittlere Wert von D₀ am offenen Ringe = 1,03 D. – Die Einzelwerte von ρ₀ lassen sich aus den obigen Gleichungen berechnen, wonach ρ/ρ₀ = 1 – f (1 – cos ω) a₁³/a³ 5,6 ρ ist, nämlich ρ₀ = ρ für ω = 0; ρ₀ = 1,036 ρ für ω = 90°; ρ₀ = 1,036 ρ für ω = 180°.

Von den Biegungsspannungen s ist nur der Höchstwert s₁ in der Mitte des Ringes bei a₁ zu beachten. Aus s₁ · a²h/6 = M₁ = p h r² · 2 folgt a₁² s₁ = 3 p D². Nach diesem und dem früheren Schlußergebnis ist das Produkt a₁ · f = 1,33 s₁ D₂/E durch die Spannung s₁ beschränkt, während das Verhältnis a₁/f = 2,25 p E/s₁² dazu verleiten könnte, die Ringstärke a₁ möglichst groß zu wählen, um hohen Dichtungsdruck p zu erhalten. Dem widerspricht die Rücksicht auf die Erhaltung der Dichtung bei Abnutzung des Ringes. Stellt man die vorigen Gleichungen für einen um ein kleines Maß x gleichmäßig abgenutzten Ring, mit ρ_x = ρ + x, auf, so findet sich p_x = p (1 – x/a₁)³ [1 – 5,33 x a³/a₁³ (1 – cos ω)f]. Hieraus geht zunächst hervor, daß nach Maßgabe des letzten Gliedes der Dichtungsdruck aufhört, wenn die Abnutzung x einen gewissen Bruchteil von f erreicht; darum müßte hiernach der Wert von f möglichst groß, also a₁ entsprechend klein gewählt werden, um eine weitergehende Abnutzung zuzulassen, bevor es nötig wird, den Ring durch Hämmern der Innenseite, besonders an den Enden, etwas zu strecken. Weiterhin erkennt man, daß der Druck p_x nicht gleichmäßig bleibt, wie bei der Aufstellung des Momentes M vorausgesetzt worden ist. Trotzdem kann die Abnutzung ziemlich gleichmäßig erfolgen, wenn der Dampf in die Ringnut, innerhalb des Ringes, eindringen und ihn gegen die Zylinderwand drücken kann.

[592] Man kann a₁ = 0,025 D + 0,7 cm setzen, oder a₁ – 0,04 D. Die Ringhöhe ist h = 0,08 D + 0,5 cm oder = 2 a₁ Für a₁/D = 0,04 findet sich die Spannung s₁ = E a₁ f/1,33 D² = 800000 · 0,04 · 0,0475/1,33 = 1140 kg/qcm, d.i. so hoch, wie man sonst nicht zu gehen wagt. Der anfängliche Dichtungsdruck wird p = a₁ s₁²/2,25 f E = 0,6 Atmosphären.

Zum Aufbringen des Ringes über den Kolbenkörper muß man ihn aufbiegen, bis sein Krümmungsradius ρ₀ auf ρ = r + a/2. kommt. Aus 1/ρ₀ – 1/ρ = M/E J = 2 s_a/a E folgt s_a = (2 a/D – 0,03) E a/D. In der Ringmitte, mit 0,036 statt 0,03 und a/D – 0,04 zeigt sich s_a = 1400; an den Enden mit 0,00 statt 0,03 und a/D = 0.7 · 0,04 wird s_a = 1800 kg/qcm! – Stärkere Ringe, etwa a₁ = 0,05 D mit p = 1,2 Atmosphären und s₁ = 1425 kg/qcm lassen sich nicht überschieben, sondern sind in einen Kolben mit abnehmbarem Deckel einzulegen. – Zweckmäßig sollte die Verjüngung starker Ringe auf 0,5 a₁ statt 0,7 a₁ angesetzt werden. Hierfür beträgt der Integralwert, bei der Berechnung von f, 6,5 statt 5,6. Mit a₁ = 0,044 D erhält man z.B. p = 0,7 Atmosphären und s₁ = 1080, dazu bessere Erhaltung des Druckes bei der Abnutzung.

Für gleichstarke Ringe [2] mit a₂ = 0,033 D wird der Integralwert 1,5 π = 4,7, somit a₀³ f = 3,35 p D⁴/E und p = 0,42 Atmosphären; dabei ist wieder s₁ = 3 p D²/a₀² = 1140 kg qcm.

Die Kolbenreibung ist abhängig von den unbekannten Werten des Flächendruckes und der Reibziffer zwischen Ring und Zylinderwand [1] und [4].

Zu dem Dichtungsdruck p eines federnden Ringes tritt noch der Dampfdruck p_m innerhalb des Ringes hinzu, der vielleicht dem Mittelwerte des treibenden Dampfdruckes gleich und nur an dem einen nächstliegenden Ringe wirksam sein mag; anderseits wirkt an der Außenfläche des Ringes die Spannung der Feuchtigkeit in fraglicher Stärke. Die Reibziffer wird von Reymann [1] zu 0,05–0,12 angegeben, und zwar für den Dampfdruck in absoluten Atmosphären und den Druck p berechnet. Die Reibungsarbeit soll sich bei einem Versuch zu 12,5% der indizierten Arbeit ergeben haben und wird für einen Niederdruckkolben zu 2,3% berechnet. Sonst wird als Reibziffer für fettige Gußeisenflächen 0,15 und für feuchte 0,31 gesetzt. – Nimmt man den indirekten Dampfdruck pi als wirksam an einem Ring von h cm Höhe an, so wird die Reibung für einen Kolben mit zwei Ringen π D h (p_i + 2 p) μ zu der treibenden Kraft p_i π D² 4 in dem Verhältnis 4 h μ (1 – 2 p/p_i) D flehen. Mit h = 0,09 D; p = 0,5 und p_i = 2,5 als Mittelwerten und μ = 0,05 – 0,1 – 0,2 – 0,3 findet sich 2,5 – 5 – 10 – 15% Reibungsverlust. Bei Dampfhämmern scheint die Kolbenreibung noch höher zu sein [3]. Bei liegenden Maschinen kommt überdies noch die Gewichtsreibung hinzu.

Das Kolbengewicht kommt bei den Berechnungen des Massendruckes, der Reibung und der Durchbiegung der Kolbenstange in Frage (s. Kolbenbewegung).

Als Durchschnittswerte kann man im allgemeinen, für D cm Kolbendurchmesser und F qcm. Kolbenfläche, die Gewichte nach folgenden Formeln ansetzen: Gewicht des Kolbens = 0,010 F√D; Gewicht der Kolbenstange = 0,0012 F D; Gewicht des Kreuzkopfes = 0,008 F√D; Gewicht von ²/₃ der Pleuelstange = 0,001 F D. Die Summe dieser Werte stellt das Gewicht G₀ der hin und her gehenden Massen dar; auf die Kolbenfläche bezogen, ist diese Summe: für den Kolbendurchmesser D = 20 30 40 50 60 70 80 90 100 cm

= 0,12 0,17 0,20 0,24 0,27 0,30 0,34 0,37 0,40 kg/qcm. Radinger, »Dampfmaschinen mit hoher Kolbengeschwindigkeit« gibt G₀/F = 0,28 für liegende Maschinen an, und = 0,33 mit Einschluß eines Kondensatorkolbens.

Literatur: [1] Zeitschr. d. Vereins deutscher Ingen. 1896, S.85 und 120 ff. – [2] Ebend. 1901, S. 232 und 373 ff. – [3] Ebend. 1902, S. 37. – [4] Ebend. 1900, S. 1405.

Lindner.

Fig. 1., Fig. 2., Fig. 3., Fig. 4., Fig. 5., Fig. 6., Fig. 7., Fig. 8., Fig. 9., Fig. 10., Fig. 11., Fig. 12.

Fig. 13., 14., Fig. 15., Fig. 16., Fig. 17.