Kurbelwellen

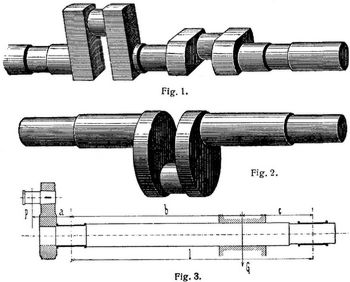
Kurbelwellen tragen Stirnkurbeln außerhalb der Lager (Fig. 3) (oder auch Handkurbeln) oder enthalten als sogenannte Krummachsen zwischen den Lagern eine oder mehrere Kurbelkröpfungen (Fig. 1 und 2).

Von den Abbildungen (Schmiedestücke der Elsässischen Maschinenbaugesellschaft in Grafenstaden) zeigt Fig. 1 eine Achse mit zwei im rechten Winkel versetzten Kurbelkröpfungen, Fig. 2 mit einer Kurbel und scheibenförmigen Kurbelarmen, die sich auf der Drehbank fertig bearbeiten lassen und zum Aufschieben von exzentrisch ausgebohrten Schwungscheiben mit Gegengewichten dienen können. Die Kurbelwellen bestehen aus Flußstahl [2] von etwa 0,3% C, 50 kg/qmm Zugfestigkeit, 30% Dehnung. Die aus dem Siemens-Martin-Ofen gegossenen Blöcke werden zu starken Wellen unmittelbar, zu mittleren und kleinen nach dem Vorwalzen ausgeschmiedet, Krummachsen zunächst rechteckig (Bd. 1, S. 67), entsprechend der Seitenansicht eines Kurbelarmes. Außen an den Kurbelarmen wird ein Dreieck ausgestoßen und das Rechteck zum Wellenschaft rund geschmiedet. Das zwischen zwei Kröpfungen liegende Wellenstück wird in Schmiedehitze verwunden, bis die Kröpfungen im richtigen Winkel zueinander stehen. Den Hohlraum zwischen den Armen einer Kröpfung sägt man auf, mit zwei Kaltsägeblättern zugleich, und flößt das Zwischenstück heraus, nachdem es längs der Innenseite des Zapfens durch mehrere Löcher dicht nebeneinander abgebohrt worden ist. Auf besonderen Kurbelwellendrehbänken [2] werden die Wellen vorgeschruppt (in diesem Zustande häufig von den Stahlwerken an Maschinenfabriken geliefert) und fertig bearbeitet. Die mehrfach gekröpften Wellen für Automobile [3] werden in ähnlicher Weise [1] fabriziert. Lokomotivachsen mit innen zwischen den Lagern liegenden Kurbelzapfen erhalten zwischen diesen ein geradliniges Verbindungsstück [4] oder auch zwei im rechten Winkel stehende Arme [5]. Die fünffach gekröpften Strohschüttlerwellen für Dreschmaschinen werden aus Rundeisen mit schrägen Uebergängen von Zapfen zu Zapfen gebogen und im Gesenk nachgerichtet. – Zum Abdrehen der Kurbelzapfen an festliegenden Krummachsen dienen auch in ringförmigen Gehäusen umlaufende Stichel [6].

Bei dem Entwurf einer Kurbelwelle schätzt man zunächst ihre Stärke zu d cm = 14 ∛N/n, um vorerst einen Anhalt für die Lagerabstände zu gewinnen, wenn dafür sonst kein Anhalt gegeben ist. Der Wellenhals im Lager neben einer Stirnkurbel (Fig. 3) ist zugleich durch Biegung und Torsion beansprucht. Die am Kurbelzapfen angreifende Kraft P bewirkt ein Biegungsmoment M_b = P a mit dem Hebelarm a, dem axialen Abstande der Kraft von der Lagermitte, und ein Torsionsmoment M_t = T R, das aus der größten auftretenden Tangentialkomponente T von P und dem Kurbelradius R zu berechnen ist. Wenn die Kraft nicht nur nahe der Totlage der Kurbel in voller Stärke wirkt, wie bei Pressen und Gasmaschinen, sondern auch während die Kurbel am Hub steht, wie bei Pumpen und Dampfmaschinen, so erreicht das Torsionsmoment den Wert P R. Wenn M_b > M_t, ist M_i = M_b + ¹/₄ M_t und wenn M_t > M_b, ist M_i = ⁵/₈ (M_b + M_t). Für den größten für irgend einen Kurbelwinkel vorkommenden Wert von M_i ist der Wellendurchmesser d aus M_i = 0,1 d³ s mit s = 300 bis 500 kg/qcm für Flußstahl zu berechnen. Die Länge des Lagers nimmt man zu etwa 1,5 d bis 2 d an und prüft den Flächendruck. Der Lagerdruck Q besteht als Resultante aus den auf das Lager kommenden lotrechten und wagerechten Drücken (s. Kurbellager). Der Wert Q/l d soll 12–16 kg/qcm betragen, ausnahmsweise bis 25 steigen. Die spezifische Lagerreibungsarbeit A = f p v = Q n/40000 l schwankt nach Grove [7] zwischen 0,2 und 1,2; er gibt eine Formel an (unter Rücksicht auf die ungleiche Druckverteilung im Lager) und findet an Beispielen die Ansichtsfläche d l des Wellenlagers vier- bis fünfmal so groß[10] wie die des Kurbelzapfens. Nach Graßmann trifft man gute Verhältnisse, wenn man A nicht konstant, sondern mit dem Durchmesser etwas anwachsend wählt und A = √d/20 für d cm setzt; für die Zapfen in Kurbelkröpfungen A = √d/3, unter Rechnung mit der vorübergehend größten Lagerdruckkraft, die vielleicht doppelt so groß ist wie der auf die Zeit berechnete mittlere Lagerdruck. Wenn eine Kurbelwelle am hinteren Ende in einen Stirnzapfen ausläuft (Fig. 3), so ist dieser nicht nach der Festigkeitsberechnung zu bemessen, sondern so viel stärker anzunehmen, daß bei der voraussichtlichen Abnutzung der beiden Lager die Welle möglichst genau senkrecht zur ursprünglichen Kurbelebene bleibt.

In der Schwungradnabe erleidet die Welle außer dem vorigen größten Torsionsmoment zugleich das hier bestehende Biegungsmoment M_b. Dieses setzt sich als Resultante aus dem Moment M_v der vertikalen Kräfte und dem Moment M_h der horizontalen Kräfte, wenn solche an der Kurbelwelle wirken, zusammen: M_b = √(M_v² + M_h²). Außer bei den dünneren Wellen, etwa unter 100 mm, für Hand- und Riementrieb, die man aus Rundeisen durchweg gleichstark abdreht, gibt man dem Nabensitz größeren Durchmesser als dem Lager, um den Sitz glatt und passend abdrehen zu können und die Schwächung durch die Keilnut auszugleichen, auch um die Durchbiegung der freiliegenden Welle möglichst zu beschränken. Diese beträgt an der Nabe (Fig. 3) für das Schwungradgewicht G und das Wellengewicht G_w, wenn die Nabe den Lagerabstand l in b und c cm teilt, f = (G + [l² + c b] G_w/8 c b) c² b²/3 E J l. Das Maß f soll höchstens 1 : 1000 der freien Länge l sein.

Mehrfach gelagerte Schwungradwellen sind bezüglich der Biegung von der Gleichmäßigkeit der Aufstellung und Abnutzung der Lager sehr abhängig. Man verteilt, um in einfacher Weise die Momente zu berechnen, die Kräfte und Gewichte an der Welle je auf die benachbarten Lager.

Schwieriger gestaltet sich die genaue Untersuchung gekröpfter Wellen [8] und [10]. Für die Berechnung gilt die Regel, daß jeder Querschnitt durch die Kräfte des auf der einen oder der andern Seite von ihm liegenden Achsenteils in gleicher Weise beansprucht wird, und zwar bewirkt eine Kraft (oder Lagerreaktion) ein Biegungsmoment mit ihrem senkrechten Abstande von der (erweiterten) Schnittebene und ein Drehmoment mit ihrer senkrechten Entfernung von der Schwerpunktsachse des geschnittenen Achsenteils.

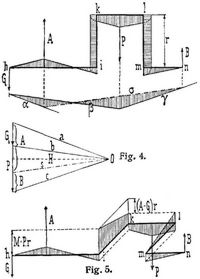
Bei der graphischen Berechnung hat man an jedem Winkelpunkte der Achsenmittellinie die Schubkraft, die algebraische Summe aller Kräfte des abgeschnitten gedachten Achsenteils, zu berücksichtigen, während sie bei geraden Achsen vernachlässigt werden darf. Als Beispiel sei die Krummachse Fig. 4 in senkrechter, Fig. 5 in wagerechter Lage, mit senkrechten Kräften berechnet. Am Schwungradsitz h wirkt das Gewicht G und das Drehmoment M. Dieses ist in Fig. 4 gleich Null, in Fig. 5 gleich P r; am Kurbelzapfen k l greift die Kraft P an; in den Lagern wirken die Drucke A und B. Man setzt die gegebenen Kräfte G und P im Maßstab 1 cm = k kg (z.B. k = 1000) aneinander (s. Fig. 4, Nebenfigur), nimmt im Abstande H cm (z.B. H = 10 cm) seitwärts den Pol O an, zieht die Strahlen a b c, legt zu b die Parallele β zwischen den Senkrechten der Angriffspunkte von G und P, von G aus weiter α parallel zu a bis zum Lager A und γ parallel zu c von P aus bis zum Lager B; schließlich ist die strichpunktierte Schlußlinie σ zwischen A und B zu ziehen, wonach die schraffierte Fläche das Seilpolygon gibt. Die Ordinaten sind an der Achse anzutragen. Sie geben die Momente für jede Stelle an, z.B. für die Ordinate von z cm der Zeichnung, wenn der Längenmaßstab 1 : l (z.B. 1 : 5) und der Kräftemaßstab 1 cm = kg angenommen war, das Moment gleich Z H k l cm kg (z.B. Z · 10 · 5 · 1000). Legt man zu σ die Parallele s vom Pol O aus, so teilt diese auf G + P die Lagerdrucke B und A ab. Bei i geht das Biegungsmoment in den Kurbelarm i k über und wirkt längs desselben als konstantes Biegungsmoment. Die Druckspannung der Arme fällt meist so gering aus, daß man sie vernachlässigen darf. In gleicher Weise erhält der Arm l m ein konstantes Biegungsmoment. Der Zapfen k l erfährt dieselbe Belastung, als ob er in der Achsenmittellinie läge.

In Fig. 5, in schräger Ansicht gezeichnet, ist das Seilpolygon, also der Verlauf der Biegungsmomente an der Achse dem vorigen wieder gleich; doch sind jetzt die konstanten Momente längs der Arme Torsionsmomente. – Das Drehmoment des Schwungrades M = P · r geht von h bis i durch und setzt sich bei i in ein Biegungsmoment des Armes i k um, so daß oben am Arm Zugspannung, längs der Unterseite Druckspannung entsteht. Die Spannungen würden längs des Armes (wie bei Fig. 4) konstant bleiben. Doch bewirkt die in i wirksame Schubkraft durch ihre Beanspruchung des Armes i k eine Aenderung des Biegungsmomentes. Die Schubkraft ergibt sich aus den Kräften des abgeschnittenen Achsenteiles zu A – G aufwärts gerichtet. Sie biegt den Arm so, daß unten Zugspannung entsteht, also dem vorigen Moment entgegengesetzt. Im Punkte k herrscht schließlich das resultierende Biegungsmoment M – (A – G) r oder (P – A + G) r. Dieses geht in den Zapfen k l als Drehmoment über und wirkt im Arme l m bei l wieder als Biegungsmoment, wobei die Zugspannung unten auftritt. Es würde im Arm Im konstant verlaufen, wenn nicht die Schubkraft G – A + P bei l ein bis m wachsendes entgegenwirkendes [11] Moment gäbe, wodurch bei m das Moment verschwindet. Dasselbe findet man, wenn man von B ausgeht und in m die aufwärts gerichtete Schubkraft B berücksichtigt. Diese ist = P – A + G, weil alle vier Kräfte an der Achse sich ausgleichen müssen. Soweit die Schubkräfte auf die axialen Strecken wirken, ändern sie das Biegungsmoment, so daß dieses je von den Eckpunkten aus nicht konstant, sondern nach der ursprünglich schon bestimmten Form des Seilpolygons verläuft. Schließlich berechnet man die Achsenstücke bezw. die Spannungen aus den Momenten in der Weise, wie unter Achsen angegeben ist (s. Bd. 1, S. 66). – Ueber Schwingungen von Kurbelwellen s. [9].

Literatur: [1] Zeitschr. f. Werkzeugmaschinen 1906/07, Heft 14 und 15. – [2] Zeitschr. d. Ver. deutsch. Ing. 1906, S. 1071, Schraml, Die Herstellung gekröpfter Wellen. – [3] Ebend. 1906, S. 344. – [4] Ebend. 1905, S. 743, und 1902, S. 1215. – [5] Ebend. 1905, S. 548. – [6] Ebend. 1903, S. 420. – [7] Ebend. 1904, S. 1777. – [8] Ebend. 1898, S. 495, Berling, Berechnung mehrmals gekröpfter Kurbelwellen für Schiffsmaschinen. – [9] Ebend. 1904, S. 564. – [10] Enßlin, M., Mehrmals gelagerte Kurbelwellen mit einfacher und doppelter Kröpfung, Stuttgart 1902.

Lindner.

Die Kurbelwelle oder Kurbelachse der Schraubenschiffsmaschine ist Torsions-, Biegungs- und Schubspannungen unterworfen. Letztere sind im Verhältnis zu ersteren klein und werden daher in der Rechnung meist vernachlässigt. Ist d der Durchmesser der Welle in Zentimetern, S die zulässige Torsionsspannung, so ist das Torsionsmoment M_t = d³ π S : 16. Das Torsionsmoment ermittelt man aus dem kombinierten Tangentialdruckdiagramm oder aus dem kombinierten Diagramm der Torsionsmomente. Das Biegungsmoment M_b ergibt sich aus M_b = Pl/6, worin l die Entfernung der beiden Wellenlagerschalen voneinander und P den größten Kolbendruck in Kilogramm angibt, wobei vorausgesetzt ist, daß l < 10 d und die Länge des Lagers mindestens gleich dem Wellendurchmesser. Da nun die Torsions- und Biegungsbeanspruchungen meist gemeinsam auftreten, so werden die Torsions- und Biegungsmomente zu einem ideellen Moment vereinigt nach folgenden Formeln:

Nach Rankine ist

nach Reuleux ist

Da man in der Praxis die Kurbelzapfen und Wellenlager meist alle gleich stark macht, um die einzelnen Teile der Maschine bequemer auswechseln zu können und die Reserveteile zu verringern, so berechnet man die Durchmesser dieser Teile nur für den hintersten Zylinder. Das ideelle Torsionsmoment bezw. Biegungsmoment muß dann aus dem entsprechenden Biegungsmoment der Kurbel und der Summe der auf die davorliegenden Kurbeln gleichzeitig stattfindenden Torsionsmomente kombiniert werden [1], [2], [6], [8].

Nach dem Board of trade ist für Compoundmaschinen mit zwei Zylindern der Wellendurchmesser in engl. Zollen

wobei D Durchmesser des Hochdruckzylinders und D Durchmesser des Niederdruckzylinders in Zollen, P den Kesseldruck in Pfund engl. und C den Kurbelradius in Zollen bedeutet. Die Konstante f schwankt für Kurbelstellung von 90–120° zwischen 2500 und 2000.

Nach den Vorschriften des Germanischen Lloyd [5] berechnet sich der Wellendurchmesser d in Zentimetern für alle Expansionsmaschinen mit nicht überhängender Kurbel nach der Formel:

Der größere aus diesen beiden Formeln sich ergebende Wert ist maßgebend. Hierin bedeutet P absoluten Kesseldruck in Kilogramm pro Quadratzentimeter, L Kurbelradius in Zentimetern, D₁ und D Durchmesser des Hoch- bezw. Niederdruckzylinders, u₁ und u die Anzahl der Hoch- und Niederdruckzylinder. Die Konstanten C₁ und C schwanken nach der Zahl der Kurbel und der Kurbelstellung, und zwar d zwischen 70 und 115, C₁ zwischen 400 und 752 [5], [6]. Als Material für diese Berechnungen ist geschmiedeter Stahl von 40–50 kg/qcm Zerreißfestigkeit und 20% Dehnung vorausgesetzt. Für Schweißeisen ist der Durchmesser um 5% zu vergrößern.

Die Kurbelwellen werden meist aus Tiegelstahl gefertigt; nur für kleinere Maschinen verwendet man noch Schweißeisen. Die zulässige Materialspannung wählt man für Schweißeisen 400–600 kg/qcm, für Tiegelstahl 600–800 kg/qcm [1]. Der Lagerdruck auf die Lager der Kurbelwelle darf 14–38 kg/qcm, derjenige auf die Lager der Pleuelstange am Kurbelzapfen 25–70 kg/qcm nicht überschreiten [6], [7]. Die Länge der Lager schwankt zwischen 1–1,5 d [2]. Die Kurbelarme werden nur auf Biegung beansprucht und meist als Träger gleicher Fertigkeit konstruiert. Ist r der Kurbelradius und P der größte Kolbendruck, so ist M_b = P r : 2. Die Kurbeln oder Krummachsen für Compoundmaschinen stehen meist im Winkel von 90° zueinander, die der dreifachen Expansionsmaschinen im Winkel von 120°, und für diese Maschinen ist die Kurbelfolge H N M die zweckmäßigste [5], [6].

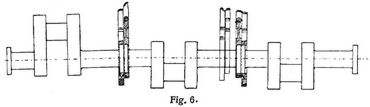
Die Kurbelwellen werden für kleinere Maschinen meist aus einem Stück geschmiedet, für größere Maschinen – bei Wellen über 25 cm Durchmesser – setzt man die Kurbelwelle aus zwei bezw. drei ganz gleichen Teilen, bestehend aus den beiden Kurbelarmen mit Zapfen und Wellenenden, zusammen und verbindet dieselben durch gewöhnliche Flanschenkupplungen mit konischen Kupplungsbolzen und Querteilen (Fig. 6) [3], [6], [7]_.; Der Raumersparnis halber werden alsdann vielfach auf den Kupplungsflanschen die Exzenter aufgesetzt. Zuweilen geschieht die Kupplung auch in den Kurbelarmen, wodurch der von den Kupplungen beanspruchte Raum gespart und ihre Lagerung in vier anstatt sechs Lagern ermöglicht wird [3], [6] (Fig. 7). Für Wellen über 40 cm Durchmesser werden die einzelnen Kurbelachsen noch aus den Wellenenden, den Armen und dem Zapfen zusammengebaut (Fig. 8). Die Kurbelarme werden meist warm[12] aufgezogen und durch Keile gesichert, während die Kurbelzapfen nur durch den Schrumpf der Kurbelarme festgehalten werden [3]. Die stärkeren Kurbelwellen werden neuerdings meist hohl hergestellt, d.h. die Wellen und Zapfen werden nach dem Schmieden ausgebohrt, Bohrung = 0,4 d. Man spart hierdurch an Gewicht und hat eine Kontrolle über die Beschaffenheit des Kernes. Von den Gegengewichten, welche früher zur Erzielung eines ruhigen Ganges der Maschine angewendet wurden, ist man abgekommen, da diese Gewichte für das Bedienungspersonal gefährlich werden können und eine beträchtliche Gewichtsvermehrung mit sich bringen. Neuerdings werden die großen Schiffsmaschinen nach der Schlickschen Anordnung, ausbalanciert [4]. Schlick schlägt die Verwendung von vier Kurbeln vor; bei dreifachen Expansionsmaschinen wählt man alsdann zwei Niederdruckzylinder, welche zwischen dem Hochdruck- und dem Mitteldruckzylinder stehen. Die Kurbeln der beiden Niederdruckzylinder stehen unter rechtem Winkel, während die des Hoch- und Niederdruckzylinders um so viel versetzt sind, daß ihre Gestängegewichte die Gegengewichte für die beiden mittleren Gestänge bilden und hierdurch die kippenden Kräfte aufheben [4].

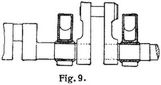
Die Kurbelwellen für Raddampfermaschinen bestehen meistens aus mehreren Teilen; entweder wählt man eine mittlere Kurbelwelle, welche die Luftpumpe treibt, und zwei äußere Radwellen, welche durch die Kurbelzapfen verbunden werden (Fig. 9), oder man lieht zwei getrennte Kurbelwellen vor, welche miteinander durch eine Flanschen- oder auch durch eine Reibungskupplung verbunden werden. In der Regel sind die Kurbelarme, welche den konisch eingesetzten und durch Mutter oder Keil gesicherten Kurbelzapfen tragen, warm aufgezogen und eventuell festgekeilt. Denselben stehen entweder gleiche Kurbelarme oder Scheiben gegenüber, welche in gleicher Weise auf der Radwelle beteiligt sind und ein Auge zur Aufnahme des freien Endes des Kurbelzapfens enthalten. Diese Konstruktion gibt der ganzen Welle etwas Beweglichkeit, was bei den heftigen Erschütterungen durch die Räder und bei der Weichheit des Schiffskörpers ganz erwünscht ist [1], [2]. Die Berechnung der Wellen auf Torsion und Biegung erfolgt in gleicher Weise wie für die Kurbelwellen der Schraubenschiffsmaschinen; für die Radwellen, bei welchen das Schaufelrad genügend unterstützt ist, wird

da dieselbe nur das halbe Biegungsmoment zu übertragen hat. Bei freitragendem Rade wirkt neben dem Torsionsmoment das Biegungsmoment, veranlaßt durch das Gewicht des Rades, welches eventuell so erheblich wird, daß die Radwelle stärker als die Kurbelwelle ausfallen kann. Der Kurbelzapfen ist nur dem Biegungsmoment ausgesetzt und kann daher schwächer gehalten werden. Für die Berechnung des Durchmessers gelten dieselben Spannungen wie für die Schraubenwellen. Der Lagerdruck kann bei der geringen Umdrehungszahl der Räder bis zu 50 kg/qcm gesteigert werden [2]. – Bei Schleppdampfern ist vielfach eine Entkupplungsvorrichtung vorgesehen, um die Manövrierfähigkeit des Schiffes zu erhöhen, so daß jedes Schaufelrad durch die zugehörige Maschinenkurbel für sich bewegt wird. Als praktische Kupplung hat sich die Reibungskupplung bewährt [3].

Literatur: [1] Busley, C., Die Schiffsmaschine, Kiel 1886. – [2] Seaton, A.E., A manual of marine engineering, London 1895. – [3] Haack, R., und Busley, C., Die technische Entwicklung des Nordd. Lloyd und der Hamburg-amerikan. Packetfahrt-Aktiengesellschaft, Berlin 1893. – [4] Schlick, O., Ueber den Einfluß des Aufstellungsortes der Dampfmaschine auf die Vibrationserscheinungen auf Dampfern, Zeitschr. d Ver. deutsch. Ing. 1894 – [5] Busley, C., Die Entwicklung der Schiffsmaschine, Berlin 1892, – [6] Bauer, G., Berechnung und Konstruktion der Schiffsmaschinen und Kessel, Berlin 1904. – [7] Wilda, H., Die Schiffsmaschinen, Hannover 1905. – [8] Bertin, L.E., Machines marines, Paris 1899.

T. Schwarz.

Fig. 1., Fig. 2., Fig. 3.

Fig. 4., Fig. 5.

Fig. 6.

Fig. 7., Fig. 8.

Fig. 9.