Polygonisierung

Polygonisierung (Polygonisieren, polygonometrische Punktbestimmung), die Bestimmung rechtwinkliger Koordinaten für Punkte in gebrochenen Linienzügen, den Polygonzügen. Zur Koordinatenberechnung werden die Strecken zwischen den Polygonpunkten, die Polygonseiten sowie die Brechungs- oder Polygonwinkel, welche die Seiten miteinander bilden, gemessen. Ein System von einer Anzahl unter sich verbundener Polygonzüge bildet das Polygonnetz. Es ist die Grundlage der Klein- oder Stückvermessung und wird bei ausgedehnten speziellen Landesvermessungen an eine Triangulation angeschlossen. Eine Kleinmessung geringen Umfanges kann auch auf einem geschlossenen Polygon gegründet werden, wenn der Anschluß an eine Triangulation nicht möglich ist. Man bezeichnet als Hauptzüge solche Züge, die zwischen trigonometrischen Punkten liegen oder das geschlossene Polygon bilden, und als Nebenzüge diejenigen Züge verschiedener Stufenfolge, die auf Polygonpunkten anfangen und endigen. Ueber Geschichtliches mit weiteren Literaturangaben s. [2]. Polygonzüge in Gruben s. Grubenmessungen und Markscheidekunde, ferner Bussolenzug und Tachymetrie.

Es möge hier auch die Bestimmung geographischer Koordinaten für Polygonzüge mit sehr langen Strecken, z.B. für die Traversen der Vermessungen in den Vereinigten Staaten von Nordamerika, erwähnt werden. Diese Art der Punktberechnung fällt jedoch nicht in den Rahmen dieser Besprechung.

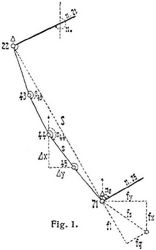
1. Der Polygonzug. Fig. 1 zeigt ein Beispiel für einen Polygonzug zwischen den trigonometrischen Punkten 22 und 71. Außer den rechtwinkligen Koordinaten dieser beiden Punkte[184] sind die der trigonometrischen Anschlußpunkte 21 und 25 gegeben. Bei gegenseitiger Sichtbarkeit hätten auch die beiden erstgenannten Punkte einer für den andern als Anschlußpunkte gewählt werden können. Gemessen sind die in der Rechnungsfolge gezählten, rechtsläufigen Brechungswinkel ß auf dem Anfangs- und Endpunkte und auf allen Polygonpunkten, z.B. ß₄₃, und die Strecken s, z.B. 44–45. Als Anfangspunkt können beide Punkte gewählt werden. Zunächst werden die Richtungswinkel n_o und n_e der in Fig. 1 stark gezeichneten Verbindungslinien 21–22 und 71–25 aus den Koordinaten dieser Punkte berechnet (s. Koordinaten, geodätische). Danach sind die Richtungswinkel n der Strecken, z.B. n₄₄, herzuleiten nach n_n = n_n – 1 + ß_n ± 180° + vß, worin vß eine Verbesserung bedeutet. Ihre Anbringung wird notwendig infolge eines Widerspruchs, der bei Vergleichung der Summe der Brechungswinkel [ß] mit der Differenz n_e – n₀ auftritt. Der Widerspruch fß rührt her zu einem geringen Teil aus den gegebenen Anfangs-, End- und Anschlußpunktkoordinaten, die bei der Berechnung zwar unveränderlich als fehlerfrei eingeführt werden, dies in Wirklichkeit aber nicht sind, und hauptsächlich aus den Fehlern der gemessenen Brechungswinkel. fß = n_e – n_o + m 180° – [ß] und, da Gleichheit der Fehler aller Brechungswinkel angenommen werden kann, für alle Richtungswinkel vß = fß : z, unter z die Anzahl aller vorkommenden Brechungswinkel verstanden; m ist eine ganze Zahl, die um zwei Einheiten oder ein Mehrfaches von zwei Einheiten von z verschieden sein kann. Nach Ausführung der Verbesserung ist n_e = n_o – m 180° + [ß] + zvß (Rechenprobe). Nunmehr werden die Koordinatenunterschiede von Punkt zu Punkt bestimmt nach Δ y = s sin n und Δ x = s cos n. Werden die Summen [Δ y] und [Δ x] mit den Unterschieden y_e – y_a und x_e – x_a der Ordinaten und Abszissen der End- und Anfangspunkte verglichen, so zeigen sich abermals Widersprüche fy = y_e – y_a – [Δ y] und fx = x_e – x_a – [Δ x]. Die Ursache dieser Widersprüche sind wie bei fß die Fehler der gegebenen Koordinaten und die Fehler der Brechungswinkel sowie außerdem noch die Streckenfehler. Die Widersprüche werden getilgt durch Zulage von Verbesserungen vy und vx zu den berechneten Koordinatenunterschieden mit den Ergebnissen Δ y,= Δ y + v_y und Δ x = Δ x + v_x sowie [Δ y] = y_e – y_a und [Δ x] = x_e – x_a (Rechenprobe). In geradlinigen Zügen und näherungsweise auch in gestreckten Zügen mit Brechungswinkeln von nahezu 180° lassen die aus der Winkel- und der Streckenmessung herrührenden Fehler sich in den Querrichtungsfehler fq und den Längenfehler fl zerlegen. Zwischen diesen und den Koordinatenfehlern fy und fx bestehen die Bezeichnungen:

und

worin

fq und fl können auch genügend genau graphisch bestimmt werden durch Eintragen von fy und fx in großem Maßstab in eine Polygonnetzkarte und Projektion der Abweichungen auf die Zugrichtung (s. Fig. 1 bei Punkt 71). Den Wert

nennt man den linearen Gesamtfehler; fq : S ist der relative Querrichtungsfehler und fl : S ist der relative Längenfehler. Die Koordinatenfehler fy und fx werden in der Regel durch Näherungsverfahren ausgeglichen. Von diesen sollen die gebräuchlichsten angegeben werden. Die Koordinatenverbesserungen für die einzelnen Punkte werden berechnet: a) mit dem relativen Querrichtungsfehler und dem relativen Längenfehler nach vy = (fl Δ y + fq Δ x) : S und vx = (fl Δ x – fq Δ y) : S; b) nach den absoluten Werten der Koordinatenunterschiede vy = fy Δy_abs : [Δy_abs] und vx = fx Δ x_abs : [Δ x_abs]; c) nach den Koordinatenunterschieden unter Berücksichtigung der Vorzeichen nach vy = fy Δ y : [Δ y] und vx = fx Δ x : [Δ x], d) nach den Streckenlängen nach vy = fys : [s] und vx = fxs : [s]. Die unter b) bis d) angegebenen Verfahren haben im allgemeinen eine Aenderung der bereits ausgeglichenen Richtungswinkel zur Folge, während das Verfahren a) neben einer Verlängerung oder Verkürzung des Zuges nur eine Aenderung der Abschlußwinkel auf dem Anfangs- und Endpunkte bewirkt. Bei gestreckten Zügen sind die Ergebnisse der vier Verfahren annähernd gleich; bei Zügen, die von der gestreckten Form abweichen, ist das Verfahren a) am meisten zu empfehlen. Eine Ausgleichung nach der Methode der kleinsten Quadrate wird seiten angewendet, da sie für stark ausbiegende Züge wegen der Schwierigkeit der Gewichtsbestimmung nicht durchführbar und für gestreckte Züge nicht erforderlich ist. Ueber solche Ausgleichungen s. [8]. Starke Ausbiegungen lassen sich häufig durch Einlegung von trigonometrischen Punkten niederer Ordnung, den Beipunkten, vermeiden [4]. Ist dies nicht möglich, so müssen die Winkel und Strecken besonders scharf gemessen werden. Weitere Fehlerverteilungsverfahren s. [2]–[5]. – Die Koordinatenberechnung wird in einem geeigneten Formular ausgeführt, und zwar in der Regel logarithmisch, je nach Erfordernis vier-, fünf- oder sechsstellig, ferner mit Hilfe von Koordinatentafeln (s.d.) oder endlich mit den natürlichen Zahlen der trigonometrischen Funktionen unter Benutzung einer Multiplikationstafel oder einer Rechenmaschine. Weiteres s. [1]–[5]. – Da die Richtungswinkel von den unveränderlichen Anfangs- und Endrichtungswinkeln abhängig sind und durch Uebertragung der Brechungswinkel gebildet werden, ist die Größe des Fehlers eines Streckenrichtungswinkels proportional √(r – r² : z) worin r die Ordnungszahl des Brechungswinkels bezeichnet. Der Fehler wächst gegen die Mitte des Zuges und nimmt von da gegen das Ende wieder ab. Er ist in der Zugmitte um so größer, je größer die Anzahl z aller Brechungswinkel ist. Es sind daher unter Beachtung praktischer Grenzen möglichst wenig Brechpunkte in einem Polygonzug anzuordnen, im Durchschnitt etwa fünf, nicht über zehn. Wegen der Bildung der Koordinatenunterschiede nach s sin n und s cos n und deren Aufsummierung von Punkt zu Punkt ist nur dann, wie oben bereits ausgeführt, eine genügende Trennung der Fehler von n und s möglich, wenn die Größe der Brechungswinkel nahezu 180°[185] ist. Daher ist eine gestreckte Form der Züge zu wählen. Um diese Form zu erreichen, werden zuweilen besondere Hilfsdreiecke angewendet, wie in Fig. 2 bei den Punkten 8, 9 und 10 zur Umgehung einer Wegekrümmung. Für die Bemessung der Streckenlängen sind maßgebend die Geländeform und die Rücksichtnahme auf die Beschaffung eines genügend engen Festpunktsystems für die Kleinmessung und auf den Anschluß der später auszuführenden Fortführungsmessungen an dieses System. Strecken von 50–300 m, im Mittel 150 m, sind zweckmäßig. Gleiche Länge der Strecken eines Zuges in anzustreben, da dann auf Gleichartigkeit sowohl der Streckenmeßfehler unter sich als auch der Winkelmeßfehler im Zuge gerechnet werden kann. Die Polygonpunktorte müssen so ausgewählt werden, daß sie für die Streckenmessung günstig liegen und scharf sowie dauerhaft bezeichnet werden können; die Punktmarken sollen gegenseitig sichtbar sein. Weiteres über die Theorie der Polygonzüge s. [2], [5] und [8].

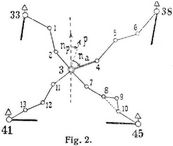
2. Polygonnetz, Knotenpunkt, Zugverzweigung. Die Anordnung und Gliederung des Polygonnetzes wird in erster Linie durch seinen Zweck bestimmt, eine Unterlage für die Kleinmessung zu bilden. Bei der Anlage ist nicht nur auf die Urvermessung Rücksicht zu nehmen, sondern auch auf die späteren Fortführungsmessungen (s. Kataster). Die Züge folgen den Wegen, Wasserläufen und Grenzlinien und umschließen einzelne Geländeabschnitte derart, daß die Linienabsteckung der Kleinmessung auf engbegrenzte Gebiete, wie Gewannen und Blöcke, beschränkt bleibt. Die Anordnung ist naturgemäß abhängig von der Geländebeschaffenheit und von der Summe der aufzumessenden Einzelheiten. Diese ist verschieden in Wald- und Feldfluren, in Ortslagen mit einzelnen Gebäuden und städtischen Bezirken, in Neustadt und Altstadt. In [4] sind Erfahrungssätze für die Anzahl der Polygonpunkte angegeben, die je nach Geländeschwierigkeit und Parzellierung erforderlich ist. Für die Anordnung des Polygonnetzes ist grundsätzlich zu unterscheiden, ob es als ein unabhängig von den Vermessungsobjekten dauernd für sich bestehendes Liniensystem aufgefaßt wird, oder ob es in innige Beziehung zu den Vermessungsobjekten gebracht und mit diesen erhalten werden soll. Das erste Prinzip liegt z.B. dem Verfahren der preußischen Katasterverwaltung zugrunde [4], das letztere z.B. dem Verfahren der badischen Katasterverwaltung [3]. Eine zweckmäßige Vereinigung beider Verfahren ermöglicht, die beiderseitigen Vorteile auszunutzen. Treffen mehrere Züge in einem noch nicht bestimmten und auch trigonometrisch nicht bestimmbaren Punkte, einem Knotenpunkte, zusammen (Fig. 2), so kann es zweckmäßig sein, sie gemeinsam zu berechnen. Aus allen Zügen wird zunächst der mittlere Richtungswinkel einer Strecke, z.B. n_a in Fig. 2 oder besser der mittlere Richtungswinkel n_p der Geraden nach einem entfernten Zielpunkte P unter Berücksichtigung von Gewichten abgeleitet. Als Gewichte kann man die reziproken Werte der Anzahl der Brechungswinkel 1 : z wählen. Auf den mittleren Richtungswinkel werden die Streckenrichtungswinkel ausgeglichen. Danach berechnet man das allgemeine arithmetische Mittel der Koordinaten des Knotenpunktes (3 in Fig. 2) aus allen Zügen, wobei die Gewichte etwa umgekehrt proportional der Zuglänge, wenn nötig auch noch nach Schwierigkeit der Messung und Anzahl der Brechungspunkte angesetzt werden können. Endlich wird die Punktberechnung in den Zügen auf die Knotenpunktkoordinaten abgeschlossen. Die trigonometrische Bestimmung eines Punktes ist der als Knotenpunkt vorzuziehen. Weiteres s. [2], [4] und [5]. In [5] ist auch die einheitliche Berechnung von Knotennetzen und Zugverzweigungen nach dem allgemeinen arithmetischen Mittel und nach der Methode der kleinsten Quadrate eingehend behandelt. – Die Berechnung der Haupt- und Nebenzüge des Polygonnetzes einer Gemarkung wird in geeigneter Stufenfolge ausgeführt. Bei städtischen Vermessungen kommen als letzte Stufe besondere Züge in Hofräumen hinzu, für die ein geregelter Anschluß seiten ausführbar ist. Eine Probe läßt sich dadurch beschaffen, daß passende Zielpunkte, wie Blitzableiter und Turmspitzen, von Punkten mehrerer Züge aus angezielt werden. Sobald mehr als zwei Anschnitte vorliegen, ist eine Probe gewonnen. Weiteres s. [6]. – Für die Berechnung der Polygonnetze in geschlossenen Polygonen ohne trigonometrische Unterlage sind die obigen Ausführungen ebenfalls gültig. Wegen der Wahl der Abszissenachse s. Koordinaten, geodätische. Weiteres s. [2] und [5].

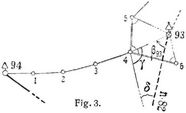
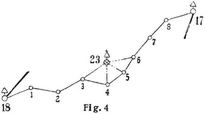
3. Anschluß an unzugängliche Dreieckspunkte. Da viele trigonometrische Punkte (s. Triangulierung) insbesondere in Ortschaften, wie Türme, Blitzableiter, Fahnenstangen und Schornsteine, für die unmittelbare Messung der Abschlußwinkel und Strecken nicht zugänglich sind, so muß deren Messung indirekt erfolgen. Hierbei ist zu unterscheiden, ob zum Abschluß der Brechungswinkel andre Dreieckspunkte benutzt werden können oder nicht. – Fig. 3 zeigt ein Beispiel. Der Kirchturm 93 ist unzugänglich; die Anschlußstrecke 4–93 wird doppelt bestimmt aus den Dreiecken über den Linien 4–5 und 4–6 nach dem Sinussatz der ebenen Trigonometrie (s.d.). Der Anschlußwinkel β₉₃ auf 93 ergibt sich nach Messung des Winkels γ aus dem Dreieck 4–93–82 ebenfalls nach dem Sinussatz, nachdem die Seite 93–82 aus den Koordinaten dieser Punkte berechnet worden ist. Eine Probe wird gewonnen, wenn eine zweite Anschlußrichtung, z.B. auf 4 oder 5, möglich ist. Ist überhaupt keine Anschlußrichtung sichtbar, wie dies z.B. in enggebauten Ortslagen häufig vorkommt, so ist in der Regel eine Zusammenfassung von zwei oder mehr Zügen mit gemeinschaftlichem Winkelabschluß nach Andeutung von Fig. 4 möglich. In manchen Fällen, besonders bei kurzen Anschlußstrecken, ist es vorteilhaft, die Koordinaten des Dreieckspunktes auf einen Bodenpunkt zu übertragen,[186] der dann an Stelle des hochgelegenen, unzugänglichen Dreieckspunktes tritt (sogenanntes Herablegen eines Dreieckspunktes). In diesem Falle sind nach Ableitung des Richtungswinkels und der Entfernung für die Anschlußstrecke, z.B. 93–4 in Fig. 3, die Koordinatenunterschiede 93–4 und damit die Koordinaten von 4 zu rechnen (s. Koordinaten, geodätische), wobei für eine Probe durch doppelte Ableitung zu sorgen ist. Für die Ausführung der Messung ist zu beachten, daß diese Uebertragung im Prinzip fehlerfrei, d.h. so genau wie möglich, zu erfolgen hat, während für den indirekten Anschluß die Genauigkeit der übrigen Strecken und Winkel genügt.

4. Die Vermarkung der Polygonpunkte muß derart beschaffen sein, daß die Marke den Punktort genügend scharf angibt und dauernd Zweifellos erhalten werden kann nicht nur während der Polygonisierung und Stückvermessung, sondern auch für alle späteren Ergänzungsmessungen. Die Ausführung der Vermarkung ist je nach den Verhältnissen verschieden. In [4] ist für die preußische Katastervermessung ein unter der Erdoberfläche mit lotrechter Mittellinie versenktes Drainrohr von 4,5 cm lichter Weite vorgeschrieben. Besser ist eine behauene Steinsäule mit einem aufgemeißelten Kreuz, mit einer Lochmarke oder mit einem eingelassenen Eisenbolzen als Tagesmarke und eine unterirdische, zentrische Versicherung durch ein Drainrohr oder ein eisernes Rohrstück, das aus billig zu beschaffenden, gebrauchten Gas- oder Siederöhren hergestellt werden kann. In Städten kommen versenkte, durch Straßenkappen geschützte Rohre und in das Pflaster oder den Bürgersteig eingetriebene oder gemeißelte Zeichen zur Anwendung. Zur sicheren Wiederherstellung der Vermarkung nach etwaiger Beschädigung oder Entfernung durch Tiefbauarbeiten werden Bolzen als Nebenmarken an den Hausfronten angebracht. Weiteres s. [2] und [6].

5. Die Winkel- und Streckenmessung. Für die Winkelmessung genügt die Genauigkeit, die ein kleiner Theodolit mit 30'' oder 20'' Nonienangabe bei ein- bis zweimaliger Beobachtung in beiden Fernrohrlagen gewährt. Von besonderer Wichtigkeit ist die scharfe Zentrierung des Instruments und der Signale auf den Punktmarken. Eine Abweichung von ± 1 cm in der Aufstellung von Instrument und Signal erzeugt z.B. bei 100 m Entfernung Richtungsfehler von je ± 20''. Da die scharfe Zentrierung des Instruments mit dem Schnurlot bei bewegter Luft Schwierigkeiten macht, werden andre Ablotvorrichtungen mit Erfolg angewendet. Sehr geeignet ist das sogenannte feste Lot, ein mit einer Dosenlibelle einzurichtendes, mit dem Stativ und der Instrumentachse verbundenes Rohr; ferner werden auch optische Ablotinstrumente (s.d.) benutzt. Zur Bezeichnung der Zielpunkte sind besonders Zielstäbe aus etwa 8 mm starkem Möbelrohr geeignet, die von einem einfachen eisernen Dreifuß gehalten und mit dem Schnurlot oder besser mit einer Anlegelibelle senkrecht gestellt werden [7]. Für städtische Arbeiten empfiehlt sich die gleichzeitige Verwendung von mindestens drei Stativen, die über den Punktmarken aufgeteilt nacheinander als Träger des Instruments und besonderer Zielscheiben dienen. Die Streckenmessung wird in der Regel mit Meßlatten oder mit dem Meßbande ausgeführt. Für städtische Arbeiten ist die Verwendung von Meßlatten mit Endschneiden und mit Zentimeterteilung zu empfehlen. Auf Maßvergleiche mit dem Normalmaß ist Bedacht zu nehmen (s. Komparator). Die Messung wird stets doppelt, hin und her, ausgeführt. Weiteres s. Längenmessung. In besonderen Fällen kann an Stelle der unmittelbaren Längenmessung die Distanzmessung treten (s. Bd. 2, S. 787, und Bd. 5, S. 408).

6. Regelmäßige Längenfehler und grobe Fehler. Ueber das Auftreten von regelmäßigen Fehlern bei der Längenmessung s.d. In einer auf Triangulierung gegründeten Polygonisierung können regelmäßige Längenfehler noch entstehen aus einer Verschiedenheit der Längenmeßinstrumente für die Polygonisierung und die Basismessung der Triangulation. Man kann das Vorkommen und die Größe von solchen Fehlern feststellen durch Berechnung der relativen Längenfehler fl : S für eine Anzahl günstig gelegener, gestreckter Polygonzüge zwischen trigonometrischen Punkten. Wenn die berechneten Werte nahezu gleich sind und gleiche Vorzeichen haben, sind regelmäßige Fehler vorhanden. Es ist unter Umständen zweckmäßig, aus der Summe dieser Werte und ihrer Anzahl u einen Mittelwert r = [fl : S] : u zu bestimmen und den Polygonstrecken vor der Koordinatenberechnung Verbesserungen zuzulegen nach s + vs, wobei vs = rs ist. Die Anwendung des unter 1. a) besprochenen Ausgleichverfahrens macht diese Arbeit entbehrlich. – Ist in einem Polygonzüge ein grober Winkelfehler oder ein grober Längenfehler vorgekommen, so läßt sich ermitteln, wo die Fehler liegen. Ein grober Winkelfehler wird gefunden durch Berechnung des Zuges von beiden Endpunkten aus. Er liegt in dem Polygonpunkt, dessen Koordinaten aus beiden Rechnungen nahezu gleich hervorgehen. Zum Aufsuchen eines groben Längenfehlers in einer Strecke wird der Zug vom Anfangspunkt aus berechnet. Die Berechnung ergibt dann nicht die genäherten Werte der Koordinaten des Endpunktes, sondern der Koordinaten eines andern Punktes. Der Richtungswinkel der Verbindungslinie dieses Punktes mit dem Endpunkte ist näherungsweise gleich dem Richtungswinkel der Strecke, deren Längenbestimmung den Fehler enthält. Graphische Verfahren, die den rechnerischen entsprechend ausgeführt werden, also Aufzeichnen der Anfangs-, End- und Anschlußpunkte nach ihren Koordinaten und Auftragen des Zuges mit Transporteur und Maßstab, führen ebenfalls zum Ziel.

7. Genauigkeit und Fehlergrenzen. Die allgemeine Anforderung an die Genauigkeit der Polygonisierung ist, daß ihre Fehler gegenüber denjenigen der Kleinmessung außer Betracht bleiben können. Eine Beurteilung der Genauigkeit lassen die relativen Querrichtungsfehler fq : S und die relativen Längenfehler fl : S in den verschiedenen Zügen zu. Für den Abschlußfehler der Brechungswinkel gelten verschiedene Fehlergrenzen. Bei der preußischen Katasterverwaltung[187] gilt z.B. nach [4] 1,5' √z, entsprechend einem mittleren Gesamtfehler von ± 0,5' für jeden Brechungswinkel, bei der Katastervermessung in Elsaß-Lothringen 1,0' √(z + 1) und z.B. in Hamburg für städtische Verhältnisse 0,7' √(z + 1); z + 1 ist mit Rücksicht auf die Fehler der trigonometrischen Anschlüsse eingeführt. Die Abweichungen, die bei der doppelten Streckenmessung hervortreten, sollen nicht über einige Zentimeter hinausgehen. Amtlich ist meistens vorgeschrieben, daß diese Abweichungen sowie die Gesamtfehler f_s = √(f_y2 + f_x2) innerhalb der Fehlergrenzen bleiben, die für die Längenmessung (s.d.) aufgestellt sind.

Literatur: [1] Die Polygonisierung ist behandelt in den beim Art. Geodäsie unter [4]–[10] genannten Lehrbüchern. Die technische Durchführung mit zahlreichen Literaturangaben ist besonders dargestellt in [2] Jordan, Handbuch der Vermessungskunde, Bd. 2, 6. Aufl., Stuttgart 1904. – [3] Die amtlichen Vorschriften über die Ausführung der Polygonisierung sind angegeben beim Art. Kataster, Bd. 5, S. 409. – Für Preußen gilt [4] IX. Anweisung für die trigonometrischen und polygonometrischen Arbeiten u.s.w., 3. Aufl., Berlin 1903. – Ausführliche Erläuterungen hierzu gibt [5] Gauß, F.G., Die trigonometrischen und polygonometrischen Rechnungen, 3. Aufl., Halle 1906. – Wegen einiger städtischen Polygonisierungen sei verwiesen auf [6] Zeitschr. für Vermessungswesen, Stuttgart 1881, S. 16; 1888, S. 193, 241 (Berlin); 1887, S. 314 (Karlsruhe), S. 65 (Altenburg); 1889, S. 52 (Bremen); 1893, S. 129 (Straßburg i. E.); 1895, S. 112 (Leipzig). Weitere Literaturangaben s. die jährlichen Literaturberichte der Zeitschr. f. Vermessungswesen. – [7] Zeitschr. für Vermessungswesen 1892, S. 155; 1893, S. 218. – [8] Fenner, ebend. 1887, S. 249; Ferber, ebend. 1907, S. 618.

(† Reinhertz) Hillmer.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.