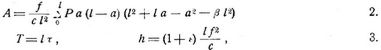Bogen, durchlaufende

Bogen, durchlaufende (kontinuierliche), im Gegensatze zu einfachen Bogen (s.d.), sind Bogenträger, die sich ungetrennt über zwei oder mehrere Oeffnungen erstrecken. Es gilt also für sie zunächst das über Bogen (s.d.) im allgemeinen Gesagte. Balken gegenüber kann neben (theoretisch) geringerem Materialverbrauch besonders der ästhetische Gesichtspunkt geltend gemacht werden, mehreren einfachen Bogen gegenüber aber läßt sich anführen, daß die Zwischenstützen bei Anordnung horizontal frei verschiebbarer Auflager (s.d.) nur Vertikal drücke aufzunehmen haben, womit dieselben schmaler gehalten werden können und der Fundamentboden geringere Beanspruchungen erleidet.

Erster Fall.

Für vollwandige Bogen kam zunächst der durchlaufende Bogen Fig. 1 in Frage [1], den man sich aus mehreren einfachen Bogen mit Kämpfergelenken (s. Bogen, einfache) dadurch entstanden denken kann, daß die Gelenke über den Zwischenstützen vereinigt und (durch Rollenlager u.s.w.) horizontal frei verschiebbar gemacht werden, abgesehen von der Reibung, die hier mit ebensoviel Recht wie bei durchlaufenden Balken vernachlässigt werden kann. Bei dieser Trägerart hat man in jeder Oeffnung die Endmomente

M = 0, M' = 0,

1.

so daß in den Gleichungen für beliebige Bogen (s.d.) nur der Horizontalschub H statisch unbestimmt bleibt.

Wir drücken H wie bei einfachen Bogen mit zwei Gelenken und ohne Gelenk unter Voraussetzung symmetrischer Parabelbogen von konstantem (mittlerem) c = J cos φ in jeder Oeffnung aus, womit auch ε, β durch die Formeln 22 unter »Bogen, einfache« ausgedrückt sind und β fast immer vernachlässigt werden kann. Indem wir neben den dort eingeführten Bezeichnungen in jeder Oeffnung l zur Abkürzung setzen:

ergibt sich ([7], § 21) der Horizontalschub durch beliebige Belastung aller Oeffnungen:

durch beliebige Temperaturänderungen τ der einzelnen Oeffnungen (bei Zunahme τ positiv):

[154] und durch eine etwaige (unbeabsichtigte) Aenderung ΔL ihrer Gesamtlänge L = Σ l (bei Zunahme ΔL positiv):

Die Summen Σ in 4.–6. beziehen sich auf sämtliche Oeffnungen, Elastizitätsmodul E und Ausdehnungskoeffizient α in denselben sind als gleich vorausgesetzt. Speziell für eine innerhalb einer ganzen Oeffnung gleichmäßig verteilte Last von u pro Längeneinheit hat man nach 2. in dieser Oeffnung (vgl. Belastung der Träger):

Gleichlange Oeffnungen. Werden die Bogenabschnitte in allen Oeffnungen mit gleichen l, f und gleichen Dimensionen (Querschnitte u.s.w.) hergestellt, dann erhält man mit der Bezeichnung:

den Horizontalschub durch beliebige Belastung aller Oeffnungen:

und speziell für beliebige gleichmäßig verteilte Lasten u in den einzelnen Oeffnungen

Der Horizontalschub durch beliebige Temperaturänderungen τ den einzelnen Oeffnungen wird:

und der Horizontalschub durch eine Aenderung ΔL ihrer Gesamtlänge L:

Diese Ausdrücke ergeben bei Belastung und Temperaturänderung nur einer Oeffnung sowie für eine bestimmte Längenänderung ΔL gerade 1/n so große Werte als bei gleicher Belastung, Temperaturänderung und Längenänderung eines einfachen Bogens mit Endgelenken von den Verhältnissen der Bogenabschnitte in den einzelnen Oeffnungen. Sind jedoch die Belastungen und Temperaturänderungen in allen Oeffnungen dieselben, dann hat man in 9.–12.:

womit jene Gleichungen vollständig mit den entsprechenden für den einfachen Bogen mit zwei Gelenken übereinstimmen (vgl. Bogen, einfache, Formeln 17., 20., 18., 19.).

Bewegte Last. In jeder bestimmten Oeffnung sind die Grenzwerte der Beanspruchungen durch Belastung dieser Oeffnung l ganz so zu berechnen, als wenn der Trägerabschnitt der Oeffnung ein einfacher Bogen mit zwei Gelenken wäre, nur daß die Gleichung der Kämpferdrucklinie S jetzt bei Vernachlässigung von β ist:

wobei in den Ausdrücken 3. auch ε vernachlässigt werden kann. Mit jenen Grenzwerten sind die durch die Temperaturänderungen und die Belastung außerhalb l erzeugten Grenzwerte, die den betreffenden Grenzwerten von H entsprechen, so zu kombinieren, daß möglichst ungünstige (möglichst weit auseinander gelegene) Grenzwerte im ganzen entstehen. Näheres, auch über die Grenzwerte der Stützenreaktionen, s. [7], 21.

Weitere Fälle.

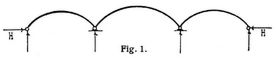
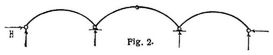
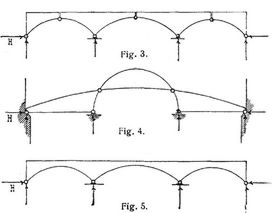
Wird bei den bis jetzt betrachteten Bogen in einer der n Oeffnungen ein Zwischengelenk angeordnet (Fig. 2), so erhält man eine statisch bestimmte Trägerart; sämtliche Stützenreaktionen einschließlich des Horizontalschubs lassen sich aus rein statischen Gleichungen bestimmen, womit dann auch gleichmäßige Temperaturänderungen der Bogenabschnitte in den einzelnen Oeffnungen und kleine Aenderungen der Spannweiten keinen Einfluß auf die Beanspruchungen haben. Der Horizontalschub H ist nur von der Belastung in der Oeffnung mit Zwischengelenk abhängig und ganz so bestimmt, als ob sich in dieser ein Bogen mit drei Gelenken befände. Ueberhaupt sind die Beanspruchungen der Oeffnung mit Zwischengelenk durchaus wie für einen einfachen Bogen mit drei Gelenken zu berechnen. In den Oeffnungen ohne Zwischengelenk gelten zunächst die für Bogen im allgemeinen bestehenden Beziehungen (s. Bogen, Bogenfachwerke). Bei bewegter Last sind die Grenzbeanspruchungen in diesen Oeffnungen zunächst für H = 0 d.h. wie für einfache Balken mit frei drehbaren Enden zu berechnen (s. Balken, einfache, Balkenfachwerke). Diese Grenzbeanspruchungen sind sodann mit den durch die Grenzwerte von H allein erzeugten Grenzwerten so zu kombinieren, daß möglichst ungünstige Grenzbeanspruchungen im ganzen entstehen. Bezüglich der Stützenreaktionen und ihrer Grenzwerte s. [3] § 78, [4], A.43. – In Fig. 3–5 sind weitere Fälle durchlaufender Bogen angedeutet, wobei jedoch, wie oben, nur die Anordnung der Auflager und Zwischengelenke, nicht die Form des Trägers wesentlich ist (s. Träger). Für Fig. 3 lassen sich bei beliebig vielen Oeffnungen alle Stützenreaktionen aus[155] rein statischen Gleichungen ohne Hilfe der Elastizitätslehre bestimmen (die Trägerart ist statisch bestimmt). Für Fig. 4 muß nur der Horizontalschub aus Beziehungen der Elastizitätslehre ermittelt werden (die Trägerart ist einfach statisch unbestimmt). Für Fig. 5 dagegen hat man den Horizontalschub und sämtliche Reaktionen der Zwischenstützen oder ebensoviele voneinander unabhängige Funktionen dieser Größen aus der Elastizitätslehre zu bestimmen (die Trägerart ist bei n Oeffnungen n fach statisch unbestimmt). S.a. Bogenfachwerke.

Literatur: [1] Schmidt, Die kontinuierlichen Bogen, Wien 1878. – [2] Müller-Breslau, Ueber kontinuierliche Bogen und Balken, Wochenblatt für Architekten und Ingenieure 1884, S. 463, 470, 481, 490. – [3] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887, §§ 79–81. – [4] Weyrauch, Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, A. 42, 43 und B. 93–103. – [5] Handbuch der Ingenieurwissenschaften, Bd. 2, XII Theorie der eisernen Bogenbrücken und Hängebrücken (insbes. § 22), Leipzig 1890. – [6] Bohny, Der kontinuierliche Zweigelenkbogen, Zeitschrift des Vereins deutscher Ingenieure 1896, S. 1249, 1380. – [7] Weyrauch, Elastische Bogenträger u.s.w., München 1897, §§ 21–23. – [8] Müller-Breslau, Die graphische Statik der Baukonstruktionen II, Leipzig 1903 (insbes. §§ 10, 15). – [9] Engesser, Ueber Bogenbrücken mit elastischen Pfeilern (Bogenreihen), Zeitschrift für Bauwesen 1903, S. 311.

Weyrauch.

Fig. 1.

Fig. 2.

Fig. 3., Fig. 4., Fig. 5.