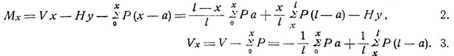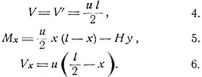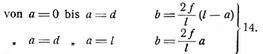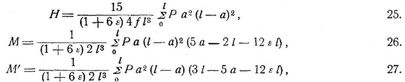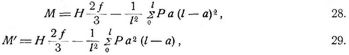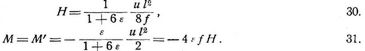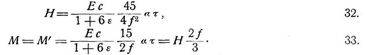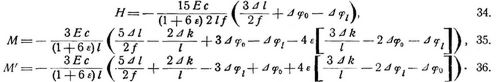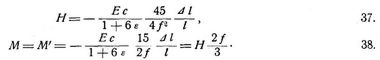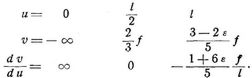Bogen, einfache

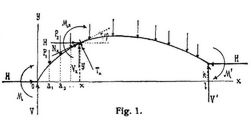
Bogen, einfache. (S.a. Bogenfachwerke, Bogen mit Zugstange.) Einfache Bogen sind Bogen mit einer Oeffnung. Es gilt also für dieselben zunächst das im Art. Bogen Gesagte, wonach die Berechnung für jede gegebene Belastung erfolgen kann, sobald der Horizontalschub H und die Endmomente M, M' bekannt sind (Fig. 1). Häufig werden an den Enden der Bogenachse Gelenke angeordnet, womit M, M' gleich 0 werden. Man bezweckt durch diese Kämpfergelenke die Auflagerdrücke an möglichst unveränderlichen Stellen auf die Kämpfer zu übertragen (s. Auflager), die Berechnung dadurch einfacher und zuverlässiger zu gestalten und günstigere Beanspruchungen zu erreichen. Beispielsweise wird der von gleichmäßigen Temperaturänderungen τ des Bogens herrührende Horizontalschub H bei gewöhnlichen flachen Bogen ohne Gelenk etwa sechsmal so groß als bei ebensolchen Bogen mit Kämpfergelenken, und die jetzigen Dimensionen der älteren Koblenzer Brücke würden ohne die Gelenkanordnung nicht einmal überall gegenüber den Einwirkungen der Temperaturänderungen allein (abgesehen von jeder Belastung) mit der üblichen Sicherheit genügen [18], S. 122. In ähnlicher Weise verstärkt sich bei Bogen ohne Gelenke der Einfluß kleiner Aenderungen der Spannweite durch Nachgeben der Widerlager, und schließlich ist die gewöhnliche Voraussetzung, bei jeder Belastung vollständige Berührung der Endquerschnitte mit den Kämpfern oder doch vollkommenes Festhalten der Endquerschnitte durch Keile, Einspannung u.s.w., bei vollwandigen Bogen mitunter nicht leicht dauernd zu erfüllen. Bei Bogen ohne Gelenke sind die Größen H, M, M' mit Hilfe der Elastizitätslehre zu bestimmen (aus den Gleichungen im Art. Biegung II.), bei Bogen mit zwei (Kämpfer-)Gelenken nur der Horizontalschub H. Durch Einschalten eines dritten Gelenks innerhalb der Spannweite kann auch H statisch bestimmt gemacht werden, womit die Berechnung weiter an Zuverlässigkeit gewinnt und gleichmäßige Temperaturänderungen wie kleine Aenderungen der Spannweite überhaupt keinen in Betracht kommenden Einfluß mehr auf die Beanspruchungen ausüben. Das Zwischengelenk pflegt bei vollwandigen Bogen in den Scheitel der Bogenachse (bei Bogenfachwerken in den Scheitel einer Gurtung) gelegt und dann auch Scheitelgelenk genannt zu werden. Nach Ermittlungen Engessers ist bei Dreigelenkbogen gegenüber Zweigelenkbogen[156] sogar eine nicht unbedeutende Materialersparnis zu erwarten [3]. Anderseits sind gegen Verwendung derselben bei Eisenbahnbrücken auf Grund mehrfacher ungünstiger Erfahrungen [10] mancherlei Bedenken laut geworden. Jedenfalls bedingt der Kräftewechsel beim Ueberschreiten des Zwischengelenks durch konzentrierte Lasten eine sorgfältige Durchbildung der Gelenkstelle [11], deren Schwäche durch die mit Temperaturänderungen und etwaigen Verrückungen der Widerlager verbundene Winkelbildung erhöht würde, so daß bei Dreigelenkbogen ebenso wie bei andern Bogen auf möglichst unnachgiebige Widerlager zu sehen ist. – Was die Form der Bogenachse betrifft, so sind meist theoretisch am vorteilhaftesten symmetrisch zur Trägermitte liegende Parabelbogen, weil für diese bei gleichmäßiger Belastung der ganzen Spannweite (annähernd für Eigengewicht allein und Vollbelastung) bei drei Gelenken keine, bei zwei Gelenken und Bogen ohne Gelenk nur kleine Momente M_x entstehen, die überdies bei Zweigelenkbogen leicht durch eine künstliche Ueberhöhung auf Null reduziert werden können (s. Horizontalschub, künstlicher, oder [15], S. 63, 77, 78, [16], S. 90, 272). Sind aber die Momente M_x = 0, so gilt das gleiche für die Transversalkräfte T_x = (d M_x)/ds (s. Bogen), während nach M_x = cN_x = 0 die Normalkraft N_x in der Achse angreift und sich gleichmäßig über den Querschnitt verteilt, womit für die erwähnten wichtigen Belastungsfälle die größten Normalspannungen in allen Querschnitten so klein als möglich werden. Neben der Parabelform kommt am meisten die Kreisbogenform vor. Häufig hat man jedoch der Bogenachse aus statischen, konstruktiven, ästhetischen oder andern Gründen eine Form gegeben, die sich durch kein einheitliches Gesetz ausdrücken läßt. Bei der älteren Koblenzer Brücke beispielsweise ist die Bogenachse bis 2,85 m horizontaler Entfernung von den Kämpfergelenken kreisförmig, von hier aus folgt sie tangential anschließenden Geraden. Bei den sichelförmigen Bogen der Maria-Pia-Brücke über den Douro (s. Bogen, S. 143, Fig. 7) wollte man die Gurtungen Parabeln einschreiben (womit auch die Achse parabolisch geworden wäre), es ergaben sich jedoch hierbei gegen die Enden hin zu geringe Höhen für die auftretenden Momente, und so änderte man die Form durch einen freien Linienzug mit Rücksicht auf gefälliges Aussehen ab. Bei Bogenträgern für Bahnhofshallen hat man sich durch Ansprüche an Raumentwicklung und monumentales Aussehen leiten lassen, bei Gewölben ist die Vermeidung erheblicher Zugspannungen maßgebend u.s.w.

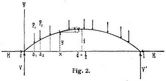
Im folgenden sollen gleiche Höhenlagen der Bogenenden vorausgesetzt werden, womit in den im Art. Bogen gegebenen Formeln k = 0 ist (Fig. 2), so daß z.B. für Bogen mit zwei und drei Gelenken die Vertikalreaktionen der Kämpfer:

und das Moment und die Vertikalkraft in einem beliebigen Querschnitt x.

Speziell für eine auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit hat man dann:

Bezüglich andrer spezieller Belastungsarten s. Belastung der Träger und [16], S. 53.

Neben den Ausdrücken von H, M, M' für beliebige Belastung und gleichmäßig verteilte Last in den wichtigsten Fällen sollen im folgenden die allgemeinsten Bedingungen für die Grenzwerte der Normalspannungen im obersten und untersten Querschnittselement bei x:

und der Transversalkraft

bei bewegter Last gegeben werden, während die Grenzwerte der Normalkraft

[157] und von H, V, V' bei möglichst starker Belastung (Eigengewicht plus Verkehrslast) und möglichst schwacher Belastung (Eigengewicht allein) des ganzen Trägers eintreten. In den beigesetzten Figuren sind die Belastungen durch Eigengewicht plus Verkehrslast (Vollbelastung, Totalbelastung) und durch Eigengewicht allein durch fette und seine Striche angedeutet. Für die Berechnung bei gleichmäßig verteilter bewegter Last genügen diese Bedingungen, während bezüglich genauerer Ermittlung der ungünstigsten Stellungen auf die Art. Grenzwerte, Einflußlinien und auf [16] verwiesen wird. Meist wird übrigens T_x bei der Dimensionierung von Bogen unberücksichtigt gelassen (vgl. Blechträger).

Bei Angabe der ungünstigsten Belastungen werden die Kernpunkte und Linien S, U, U' erwähnt. Der obere und untere Kernpunkt eines Querschnitts liegen in der Trägerebene um

oberhalb und unterhalb der Achsschicht. In den Verbindungslinien dieser Kernpunkte aller Querschnitte erhält man die obere und untere Kernlinie des Bogens, die z.B. bei rechteckigen Querschnitten (Gewölbe) das mittlere Bogendrittel begrenzen. Bei Bogen mit durchbrochenen Wandungen (Gitterbogen u.s.w.) fallen die Kernlinien annähernd mit den Gurtungsschwerlinien zusammen, während sie sonst etwas näher der Achse liegen. (Näheres s. Kernlinien.) Bei Fachwerkbogen und Gitterbogen pflegen die Normalspannungen aller Elemente eines Gurtungsquerschnitts als gleich groß angenommen zu werden, womit die unten für die Grenzwerte von σ_o σ_u angegebenen Belastungen für die Grenzwerte der ganzen Gurtungsbeanspruchungen gelten. Für den gewöhnlichen Fall symmetrisch zur Achsschicht liegender Querschnitte hat man natürlich in 7. wie in 10. e_o = e_u = e, während

das Widerstandsmoment des Querschnitts ausdrückt (s. Biegung I.). Für die Schnittlinie S und die Umhüllungslinien U, U' der Kämpferdrücke genügt es, unten ihre Gleichungen zu geben. Näheres über dieselben s. Kämpferdrücke. Die Linie S wird auch Kämpferdrucklinie genannt.

Bogen mit drei Gelenken.

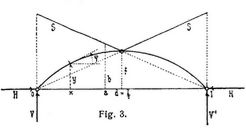
Endmomente M = M' = 0, Horizontalschub bei beliebiger Belastung (Fig. 3):

und speziell bei gleichmäßig verteilter Last von u pro Längeneinheit auf der ganzen Spannweite:

Gleichung der Kämpferdrucklinie S (Abszisse a, Ordinate b):

Die Linie ist in Fig. 3 verzeichnet.

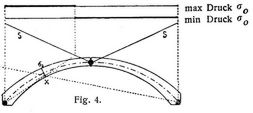
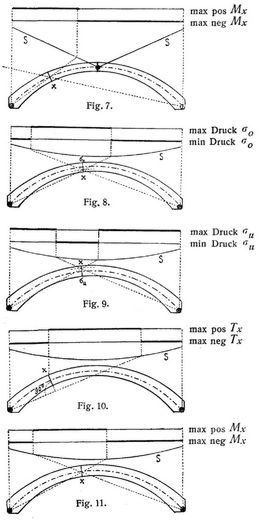
Grenzwerte von σ_o (Fig. 4, Vereinfachung s. unten). Man ziehe aus beiden Kämpfergelenken Gerade durch den unteren Kernpunkt des Querschnitts bis zu den Durchschnitten mit der Linie S. Für max Druck σ_o ist zwischen diesen Schnittpunkten, für min Druck σ_o auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

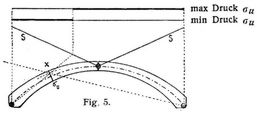
Grenzwerte von σ_u (Fig. 5, Vereinfachung s. unten). Man ziehe aus beiden Kämpfergelenken Gerade durch den oberen Kernpunkt des Querschnitts bis zu den Durchschnitten mit der Linie S. Für min Druck σ_u ist zwischen diesen Schnittpunkten, für max Druck σ_u auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

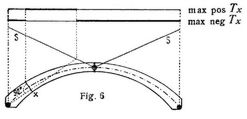
Grenzwerte von T_x (Fig. 6). Man ziehe senkrecht zur Querschnittsebene eine Gerade aus dem nächsten Kämpfergelenke bis zum Durchschnitt mit der Linie S. Es ist einmal zwischen diesem Schnittpunkt und dem obersten Querschnittspunkt (bei untenliegender Fahrbahn dem untersten), das andre Mal auf den übrigen Strecken der Spannweite möglichst stark zu belasten. Die erste Belastung liefert für Querschnitte auf der ersten Trägerhälfte den positiven, für Querschnitte auf der zweiten Trägerhälfte den negativen Grenzwert von T_x.

Häufig treten einzelne der erwähnten Durchschnitte mit der Linie S nicht innerhalb der Spannweite ein; diese liefern also auch keine wirklichen Verkehrslastgrenzen, womit jedoch an der Allgemeinheit der angeführten Regeln nichts geändert[158] wird. Für die Querschnitte unmittelbar bei den Gelenken treten die Grenzwerte von σ_o σ_u stets bei möglichst starker und möglichst schwacher Belastung der ganzen Spannweite ein. Lieber Abkürzung der Berechnung durch Verwendung der Bogenachse anstatt der Kernlinien s. unten. Mit Rücksicht auf diese Vereinfachung geben wir noch:

Grenzwerte von M_x (Fig. 7). Man ziehe aus beiden Kämpfergelenken Gerade durch den Achspunkt des Querschnitts bis zu den Durchschnitten mit der Linie S. Für max pos M_x bei der Vereinfachung auch für max Druck σ_o und min Druck σ_u) ist zwischen diesen Schnittpunkten, für max neg M_x (bei der Vereinfachung auch für min Druck σ_o und max Druck σ_u) auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

Da bei parabolischer Achse

so ist in diesem Falle bei beliebiger, gleichmäßig verteilter Last auf der ganzen Spannweite nach 5. und 13. in allen Querschnitten M_x = 0.

Bogen mit zwei Gelenken.

Endmomente M = M' = 0. Die Bedingungen für die von der Belastung herrührenden Grenzwerte von σ_o σ_u, T_x, M_x bleiben wie für Bogen mit drei Gelenken, nur daß die Kämpferdrucklinie S einen andern Verlauf hat und damit die Konstruktionen der ungünstigsten Belastung ein etwas andres Aussehen gewinnen (Fig. 8–11). Mit diesen Grenzwerten sind nun aber die von den Temperaturänderungen τ herrührenden Grenzwerte, die den H durch das größte positive und das größte negative τ entsprechen, so zu kombinieren, daß möglichst ungünstige (d.h. möglichst weit auseinander liegende) Grenzwerte im ganzen entstehen. Häufig wird τ = ± 30° C. angenommen. Die Gleichung von S und der Ausdruck von H hängen von der Form der Bogenachse und von der Veränderlichkeit des Querschnitts ab. Wir geben hier die Formeln für den gewöhnlichsten Fall, für beliebige Achsform und beliebige Querschnitte, s. [16].

Unter Voraussetzung parabolischer Achse und konstanter (mittlerer)

folgt der Horizontalschub für beliebige Belastung:

für eine Temperaturänderung τ gegen die dem spannungslosen Zustande entsprechende Normaltemperatur (bei Zunahme τ positiv):

und für eine Aenderung Δl der Spannweite (bei Zunahme Δl positiv):

Beim Zusammenwirken dieser Ursachen addieren sich die betreffenden Ausdrücke. Speziell für eine auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit wird aus 17. (s. Belastung der Träger):

Die Ausdrücke von ε, β, γ sind davon abhängig, welche Vereinfachungen bei der Integration der Biegungsformeln zugelassen werden. Häufig hat man die Beiträge von N_x und der Glieder mit dem Krümmungsradius r der Bogenachse im Nenner vernachlässigt, womit sich ergeben:

ε = 0, β = 0

welche Annahmen jedoch nicht allgemein zulässig sind. Werden jene Beiträge nicht vernachlässigt, dagegen bei Integration der Glieder mit τ, N_x, M_x/r anstatt des Parabelbogens ein Kreisbogen von gleichen l, f, also dem Radius

zugrunde gelegt, dann erhält man [16], § 24:

worin für

[159] das Verhältnis der Mittelwerte c, k (Formeln 16.) oder aber der Mittelwert von J : F gesetzt werden kann. Ersteres erscheint nach der Ableitung theoretisch etwas genauer, praktisch ergeben beide Annahmen kaum voneinander abweichende Werte von H. Bei der zweiten Annahme ist γ für Bogen mit durchbrochenen Wandungen oder mit vernachlässigter Füllung gleich dem Mittel werte von h²/4, unter h die Entfernung der Gurtungsschwerpunkte verstanden, für Bogen rechteckigen Querschnitts der Höhe h (Gewölbe) gleich dem Mittelwerte von h²/12.

Nach 22. erhält man z.B. [18] für die ältere Koblenzer Brücke (l = 98,0775 m = 11 f) ε = 0,045633, β = 0,004992, für die neue Cannstatter Neckarbrücke (l = 45,51 – 50,48 m, f = 3,695 – 4,855 m) ε = 0,016870 bis 0,010464, β = 0,001462 – 0,001287, für die Maria-Pia-Brücke über den Douro (l = 160 m, f = 42,65 m, s. Bogen) ε = 0,004287, β = 0,005447, wonach β in 17., 20. fast immer vernachlässigt werden kann. Die Gleichwie der Kämpferdrucklinie wird alsdann:

worin mit Rücksicht auf die Verwendung der Kämpferdrucklinie meist ε = 0 gesetzt werden kann. Für Näherungsrechnungen (insbesondere vorläufige Berechnungen) können auch im allgemeinen ε = 0, β = 0 und daneben anstatt des von a = 0 bis a = l zwischen l² und 5/4 l² veränderlichen Ausdrucks l² + l a – a² dessen durch die Methode der kleinsten Quadrate bestimmter Mittelwert 7/6 l² eingeführt werden, womit nach 17. für beliebige Belastung:

und nach 24. die Gleichung der Kämpferdrucklinie: b = (48/35) f. Diese ergibt sich also hierbei als eine horizontale Gerade.

Bogen ohne Gelenke.

Für diese sind der Horizontalschub H und die Endmomente M, M' von der Achsform und der Veränderlichkeit der Querschnitte abhängig, womit das gleiche bezüglich der Schnittlinie S und Umhüllungslinien U, U' der Kämpferdrücke gilt. Sind jedoch S, U, U' ermittelt (U, U' liegen bei symmetrischen Trägern symmetrisch zur Trägermitte, so daß die Ableitung von U genügt), so ergeben sich die Belastungen für die Grenzwerte von σ_o σ_u, T_x, M_x durch bewegte Last für beliebige Querschnitte wie folgt:

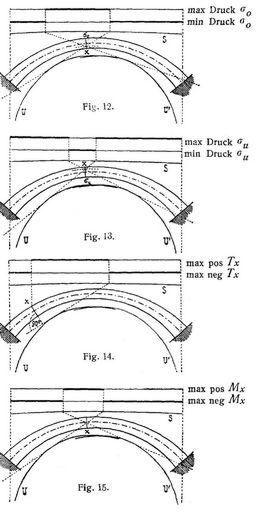
Grenzwerte von σ_o (Fig. 12, Vereinfachung s. unten). Man ziehe durch den unteren Kernpunkt des Querschnitts Tangenten an die Linien U, U' bis zu den Durchschnitten mit der Linie S. Für max Druck σ_o ist zwischen diesen Schnittpunkten, für min Druck σ_o auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

Grenzwerte von σ_u (Fig. 13, Vereinfachung s. unten). Man ziehe durch den oberen Kernpunkt des Querschnitts Tangenten an die Linien U, U' bis zu den Durchschnitten mit der Linie S. Für min Druck σ_u ist zwischen diesen Schnittpunkten, für max Druck σ_u auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

Grenzwerte von T_x (Fig. 14). Man ziehe senkrecht zur Querschnittsebene eine Tangente an diejenige der Linien U, U', an die eine solche möglich ist (für Querschnitte der ersten Trägerhälfte an U) bis zum Durchschnitte mit der Linie S. Es ist einmal zwischen diesem Schnittpunkt und dem obersten Querschnittspunkt (bei untenliegender Fahrbahn dem untersten), das andre Mal auf den übrigen Strecken der Spannweite möglichst stark zu belasten. Die erste Belastung liefert den positiven oder den negativen Grenzwert von T_x, je nachdem die Tangente an U oder an U' gezogen wurde.

Auch hier fallen häufig einzelne der erwähnten Durchschnitte außerhalb der Spannweite, so daß die betreffenden Lastgrenzen nicht zur Geltung kommen, ohne daß die obigen Bedingungen dadurch ungültig werden. Ueber Abkürzung der Berechnung durch Nichtanwendung der Kernlinien s. unten. Mit Rücksicht auf diese Vereinfachung fügen wir bei:

Grenzwerte von M_x (Fig. 15). Man ziehe durch den Achspunkt des Querschnitts Tangenten an die Linien U, U' bis zu den Durchschnitten mit der Linie S. Für max pos M_x (bei der Vereinfachung auch für max Druck σ_o und min Druck σ_u) ist zwischen diesen Schnittpunkten,[160] für max neg M_x (bei der Vereinfachung auch für min Druck σ_o und max Druck σ_u) auf den übrigen Strecken der Spannweite möglichst stark zu belasten.

Mit den von der Belastung herrührenden Grenzwerten sind, wie bei Bogen mit zwei Gelenken, die durch Temperaturänderungen τ bedingten Grenzwerte (die den H, M, M' durch das größte positive und das größte negative τ entsprechen) so zu kombinieren, daß möglichst ungünstige (d.h. möglichst weit auseinander liegende) Grenzwerte im ganzen entstehen.

Die Ausdrücke von H, M, M' geben wir wie oben bei zwei Gelenken unter Voraussetzung parabolischer Bogen von konstanten Mittelwerten 16., jedoch der hier geringeren erreichbaren Genauigkeit wegen unter Vernachlässigung von Gliedern gleicher oder kleinerer Größenordnung als β. Näheres hierüber und Formeln für beliebige Achsformen und beliebige Querschnitte s. [16]. In den folgenden Gleichungen sind r, ε durch 21., 22. bestimmt. Für eine beliebige Belastung hat man:

wonach wir auch schreiben können:

und speziell für eine auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit:

Für eine Temperaturänderung τ gegen die Normaltemperatur (bei Zunahme τ positiv) gelten:

Durch Verrückungen und Verdrehungen der Bogenenden, wobei sich l, k = 0, φ₀, φ₁ um Δl, Δk, Δφ₀, Δφ_l ändern, würden entstehen:

Wenn jedoch nur eine Aenderung Δl der Spannweite (bei Zunahme Δl positiv) oder doch sonstige Bewegungen der Stützen nur derart stattfinden, daß Δφ₀ = Δφ₁ = (Δk)/l ist, dann werden einfacher:

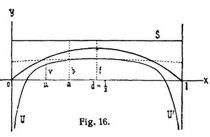
Als Gleichung der Kämpferdrucklinie S hat man (Fig. 16):

so daß S eine horizontale Gerade ist, die bei der hier zulässigen Vernachlässigung von ε um f/5 über dem Scheitel hinliefe. Für die Umhüllungslinie U gilt die Gleichung (u Abszisse, v Ordinate):

wonach für

Die Umhüllungslinie U' liegt hinsichtlich der Trägermitte symmetrisch zur Umhüllungslinie U, mit der sie bei l/2 eine gemeinschaftliche horizontale Tangente hat. Es genügt, beide Linien bis zur Mitte zu verzeichnen, da nur die Teile in den äußersten Vierteln von l Verwendung finden.

[161] Für ε = ∞ (f = 0, r = ∞ cos φ = 1) gehen alle für den Bogen ohne Gelenk und mit zwei Gelenken gegebenen Formeln in die für Balken mit beiderseits festgespannten und mit beiderseits frei drehbaren Enden gültigen Gleichungen über (s. Balken, einfache).

Vereinfachte Berechnung der Grenzwerte von σ_o, σ_u.

Je geringer die Entfernungen der Kernlinien von der Stabachse unter sonst gleichen Verhältnissen sind, um so mehr nähern sich die obenangeführten Belastungsgrenzen für

max Druck σ_o max pos M_x, min Druck σ_u,

sowie diejenigen für

min Druck σ_o, max neg M_x, max Druck σ_u.

Da nun der Einfluß der Lasten in der Nähe der Belastungsgrenzen überhaupt verhältnismäßig klein ist (an den Grenzen selbst sind die Beiträge 0), so genügt es in den meisten Fällen, die ungünstigsten Belastungen für die M_x auch als solche für die σ_o, σ_u zu verwenden, also die Kernlinien ganz aus dem Spiele zu lassen. Man erspart hierdurch nicht nur die Ermittlung der letzteren, sondern, was mehr ins Gewicht fällt, man braucht nur etwa halb so viel Belastungsfälle als bei der theoretisch genaueren Berechnung. Für die mehrfach erwähnte Cannstatter Neckarbrücke (Martinflußeisen, s.a. Blechträger) ist die genauere Berechnung in [15], die abgekürzte der Oeffnung IV in [16] durchgeführt. In der folgenden Tabelle sind die hierbei erhaltenen oberen Grenzwerte von σ_o, σ_u einer Bogenhälfte zusammengestellt, sowohl für Verkehrslast allein als im ganzen (Eigengewicht, Verkehrslast, Temperaturänderung, künstlicher Horizontalschub zusammenwirkend).

Bei den weniger wichtigen unteren Grenzwerten ergeben sich größere Abweichungen [16], § 10. Die Belastungsgrenzen weichen bei flachen Bogen oft ziemlich bedeutend voneinander ab (vgl. Tafel zu [16]), was aber deshalb keinen erheblichen Einfluß auszuüben braucht, weil die Beiträge von Lasten an den Belastungsgrenzen gleich Null sind. Die abgekürzte Berechnung, die für alle oben behandelten Bogen gilt, muß die Grenzwerte im allgemeinen etwas zu günstig liefern, da man nicht immer genau die ungünstigsten Belastungen verwendet.

Literatur: [1] Navier, Résumé des leçons sur l'application de la Mécanique, Paris 1826, p. 234. – [2] Winkler, Die Lehre von der Elastizität und Festigkeit, Prag 1867, S. 253. – [3] Engesser, Entwicklung einer Formel für das Eigengewicht schmiedeeiserner Bogenbrücken, Zeitschr. für Bauwesen 1877, S. 207. – [4] Grashof, Theorie der Elastizität und Fertigkeit, Berlin 1878, S. 251. – [5] Seyrig, Le pont sur le Douro, Mémoires de la société des ingénieurs civils, 1878, p. 741. – [6] Weyrauch, Ueber die Berechnung der Dourobrücke, Zeitschr. für Baukunde 1879, S. 421. – [7] Müller-Breslau, Theorie und Berechnung der eisernen Bogenbrücken, I: Die stabförmigen elastischen Bogen, Berlin 1880. – [8] Castigliano, Théorie de l'équilibre des systèmes élastiques, Turin 1880 (Deutsch Wien 1886), I., Chap. 9, und II., Chap. 4, 10, 11. – [9] Krohn, Resultate aus der Theorie des Brückenbaues und deren Anwendung, erläutert durch Beispiele, II: Bogenbrücken, Leipzig 1880. – [10] Zur Frage über die Anwendung von Scheitelscharnieren bei eisernen Bogenbrücken, Deutsche Bauztg. 1881, S. 351, 445, 784; 1885, S. 525. – [11] Backhaus, Allgemeine Betrachtungen über Gelenkkonstruktionen eiserner Bogenbrücken, Zeitschr. des Vereins deutscher Ingenieure 1886, S. 741, 762, 773. – [12] Ritter, Der elastische Bogen, berechnet mit Hilfe der graphischen Statik, Zürich 1886. – [13] Mantel, Der elastische Bogen unter dem Einflusse von Kräften beliebiger Richtung, Schweizerische Bauztg. 1888, II, S. 98, 111, 157, 162. – [14] Handbuch der Ingenieurwissenschaften, Bd. 2, XII: Theorie der eisernen Bogenbrücken und Hängebrücken (von Melan), Leipzig 1890. – [15] Weyrauch, Berechnung der neuen Bogenbrücke über den Neckar zwischen Stuttgart und Cannstatt, Allgem. Bauztg. 1895, S. 49, 57, 73, 85. – [16] Weyrauch, Elastische Bogenträger, ihre Theorie und Berechnung entsprechend den Bedürfnissen der Praxis, München 1897. – [17] Stark, Beitrag zur Theorie statisch unbestimmter Bogenträger, Technische Blätter 1900, S. 103 ( s.a. 1902, S. 75). – [18] Müller-Breslau, Die neueren Methoden der Festigkeitslehre, Leipzig 1904, S. 154. – S. a. Bogen, Bogenfachwerke, Bogen mit Zugstange, Bogensehnenträger, Mittengelenkbalken, Blechträger.

Weyrauch.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7., Fig. 8., Fig. 9., Fig. 10., Fig. 11.

Fig. 12., Fig. 13., Fig. 14., Fig. 15.

Fig. 16.