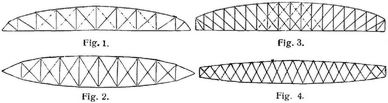
Ellipsenträger

Ellipsenträger

Ellipsenträger und Halbellipsenträger heißen Balkenfachwerke (s.d.), bei denen eine Gurtung horizontal, die andre einem Ellipsenbogen eingeschrieben ist (Fig. 1 und 3), oder bei welchen beide Gurtungen Ellipsenbogen eingeschrieben sind (Fig. 2 und 4). Bei Ellipsenträgern treffen sich der Obergurt und Untergurt an den Trägerenden (Fig. 1 und 2), während dies bei Halbellipsenträgern nicht der Fall ist (Fig. 3 und 4). Vgl. Parabelträger und Halbparabelträger.

Die ersten Ellipsenträger wurden von Laißle für die Colomakbrücke der Charkow-Krementschug-Bahn nach der Anordnung Fig. 1 angewandt die strichpunktierten Stäbe bedeuten Gegendiagonalen (s.d.), [1]; Halbellipsenträger wählte Schwedler entsprechend Fig. 3 für die Weichselbrücke bei Thorn [3] und entsprechend Fig. 4 für die Memelbrücke bei Tilsit [4]. Bei Ellipsenträgern ergeben sich gegen die Enden hin etwas größere Höhen als bei Parabelträgern, was erwünscht sein kann (vgl. Paulische Träger), auch sind im Falle schlaffer Diagonalen nicht in allen Feldern Gegendiagonalen nötig. Vgl. Schwedler-Träger. Das Aussehen ist gefälliger als das der Parabelträger und Schwedler-Träger, den Parabelträgern und Parallelträgern (s.d.) gegenüber hat man eine Materialersparnis gefunden [2]. Doch sind diese Vorzüge nicht gerade an die genaue Einhaltung der Ellipsenform gebunden. Berechnung für gleichmäßig verteilte Lasten und Radlastzüge s. [6].


Literatur: [1] Laißle und Schübler, Der Bau der Brückenträger, II, Stuttgart 1871, S. 106. – [2] Pfeufer, Der Ellipsenträger, Zeitschr. d. österr. Ingen. – u. Arch.-Vereins 1876, S. 224. – [3] Die Eisenbahnbrücke über die Weichsel bei Thorn, Zeitschr. f. Bauwesen 1876, S. 35, 197. – [4] Schwedler, Die Ueberbrückung des Memeltals bei Tilsit, Zeitschr. f. Bauwesen 1878, S. 21, 161, 363. – [5] Winkler, Theorie der Brücken, II, Theorie der gegliederten Balkenträger, Wien 1881, S. 210. – [6] Weyrauch, Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, S. 171, 177, 183, 303, 481, 483, 487.

Weyrauch.

Fig. 1., Fig. 2., Fig. 3., Fig. 4.
Fig. 1., Fig. 2., Fig. 3., Fig. 4.

http://www.zeno.org/Lueger-1904.

Игры ⚽ Поможем сделать НИР

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Träger [1] — Träger. Ein Träger ist ein materielles System (s. Bd. 6, S. 333), welches zur Aufnahme und Uebertragung von Lasten und andern äußeren Aktivkräften auf außerhalb desselben gelegene Stützen dient (vgl. Spannweite, Aktivkräfte, Belastung der Träger …   Lexikon der gesamten Technik

  • Brücken [3] — Brücken , eiserne. Darunter verlieht man alle jene Brückenbauwerke, deren Ueberbau aus Eisen hergestellt ist. Sie bilden vermöge der Häufigkeit ihrer Anwendung, der damit erzielbaren Leistungen, dann vermöge der Ausbildung ihrer Theorie und… …   Lexikon der gesamten Technik

  • Fachwerk [1] — Fachwerk (Fachwerkträger) heißen in der Ingenieurmechanik solche Träger (s.d.), die aus lauter an den Enden miteinander verbundenen geraden Stäben bestehen (Fig. 1–32). Man unterscheidet ebene Fachwerke und räumliche Fachwerke. Bei ersteren… …   Lexikon der gesamten Technik

  • Eiserne Brücken — (iron bridges; ponts en fer; ponti in ferro). Zu den E. werden alle jene Brückenbauwerke gezählt, deren Überbau aus Eisen hergestellt ist; der Unterbau (Pfeiler und Widerlager) kann dabei entweder ebenfalls aus Eisen, aus Holz oder, wie es in der …   Enzyklopädie des Eisenbahnwesens

  • Träger [1] — Träger, wagerechter, zum Tragen von Lasten bestimmter Bauteil aus Stein, Holz, Eisen oder Holz und Eisen, der auf zwei (abgesetzter T.) oder mehreren (fortgesetzter, kontinuierlicher T.) Stützen ruht oder nur an einem Ende befestigt ist (Krag… …   Meyers Großes Konversations-Lexikon

  • Fachwerke mehrfachen Systems — (mehrteiliges Fachwerk). Ein Fachwerk heißt n teilig oder n fachen Systems, wenn die Füllungsglieder (s. Fachwerk) oder doch eins über das andre solcher Füllungsglieder, die einen zusammenhängenden Linienzug bilden, durch andre gleichzeitig… …   Lexikon der gesamten Technik

  • Gegendiagonalen [1] — Gegendiagonalen. Bei Fachwerkträgern (s.d.) mit Vertikalen (Ständerfachwerke, Fig. 1–6) hat man früher häufiger als in neuerer Zeit die Diagonalen auch dann aus Flacheisen hergestellt, wenn sie in gewissen Belastungsfällen auf Druck… …   Lexikon der gesamten Technik

  • Halbellipsenträger — Halbellipsenträger, s. Ellipsenträger, Bd. 3, S. 436 …   Lexikon der gesamten Technik

  • Halbparabelträger [1] — Halbparabelträger heißen Fachwerke mit einer parabolischen Gurtung, wenn die Trägerhöhe nicht, wie bei den Parabelträgern (s.d.), nach den Auflagern hin bis auf Null herabgeht (Fig. 1–6). Die zweite Gurtung ist meist gerade (Fig. 1, 2,… …   Lexikon der gesamten Technik

  • Parabelträger [1] — Parabelträger heißen Fachwerke (s.d., Bd. 3, S. 533), deren Gurtungsachsen Parabeln mit vertikaler Achse durch die Trägermitte eingeschrieben sind und sich an beiden Enden treffen (vgl. Halbparabelträger). Da sich auch eine Gerade als Parabel… …   Lexikon der gesamten Technik

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”