- Schwere, Schweremessung
Schwere, Schweremessung. – 1901 stellte Helmert die in Bd. 8, S. 15 mitgeteilten Formeln für die normale Schwerkraft γ im Meeresniveau auf. Die Grundlage hierfür ist das Wiener Schweresystem mit dem durch v. Sterneck, v. Oppolzer und v. Orff bestimmten absoluten Werte der Schwerkraft für Wien g = 9,80876 m.sek–2. Kühnen und Furtwängler bestimmten den absoluten Wert für Potsdam zu g = 9,81274 m.sek–2 [1]. Borras glich die relativen Schweremessungen eines Netzes von Hauptstationen nach der Methode der kleinsten Quadrate aus, s. Bd. 6, S. 415, und bezog sie auf das zurzeit wohl am besten begründete Potsdamer Schweresystem. Er verwendete nicht alle vorhandenen Beobachtungen, traf vielmehr eine Auswahl nach bestimmten Grundsätzen und beschränkte die Ausgleichung auf 20 Netzpunkte mit 62 Stationen und 23 voneinander unabhängigen Beobachtungsreihen. Das Ergebnis für Wien war, vom älteren Werte in den beiden letzten Stellen abweichend, g = 9,80860 m.sek–2. Zwischen den beiden Systemen besteht also die Beziehung: Wiener System – 0,00016 m.sek–2 = Potsdamer System. Danach sind die Formeln für die normale Schwerkraft im Potsdamer System:
γ = 9,78030 (1 + 0,005302 sin2 φ – 0,000007 sin2 2φ) oder
γ = 9,80616 (1 – 0,002644 cos2 φ + 0,000007 cos2 2φ).
An Stelle der in Bd. 8, S. 16 angegebenen älteren Formeln für die Reduktion der Beobachtungswerte g benutzte Borras bei den Berechnungen die neueren Formeln 1. wegen der Meereshöhe + 10-7 3086 H und dem entsprechend 2. wegen der Anziehung der zwischen der Meeresfläche und dem Beobachtungspunkte liegenden Masse – 3 Θ 10-7 3086 H : 4 Θm; hierin Θm = 5,52 [2]. In diesem Berichte [2] sind alle bis 1909 bekannt gewordenen relativen Schweremessungen im Potsdamer System zusammengestellt. Das Verzeichnis enthält 2819 Stationen, von denen jedoch viele mehrfach aufgeführt worden sind. Für 83 Stationen liegen die Ergebnisse noch nicht vor. Aus dem Vergleiche dieser Zahlen mit den in Bd. 8, S. 16 angegebenen ersteht man die großen Fortschritte der relativen Schweremessungen. S. hierzu auch Pendelapparat, Bd. 7, S. 63.
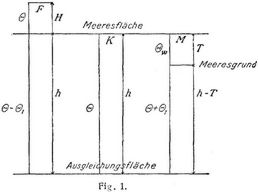
Nach Bd. 8, S. 16, ist dem Beobachtungswerte g außer den beiden oben genannten Reduktionen noch eine dritte, die topographische Reduktion, zuzufügen, um ihn mit dem normalen Werte y vergleichen zu können. Hayford und Bowie haben nun die Hypothese von der Isostasie der Erdkruste über einer Ausgleichungsfläche, s. Erde, S. 245, die für die Vereinigten Staaten von Nordamerika zutrifft, benutzt und in [3] untersucht, welchen Einfluß die nach Bodengestalt und isostatischer Ausgleichung berechnete Massenanziehung auf die Schwerkraft ausübt. Nach der genannten Hypothese ist das Gewicht der Massen zwischen der Ausgleichungs- und der Erdoberfläche bezw. der Meeresfläche bei Küsten- und Meeresörtern über der Flächeneinheit gleich. Man hat angenommen, daß die Dichte der sichtbaren Masse eines Festlandortes F gleich ist der Dichte Θ der Masse eines Küstenortes K zwischen der Ausgleichungs- und der Meeresfläche, s. Fig. 1. Dann hat die Masse eines Festlandortes zwischen der Ausgleichungs- und der Meeresfläche die Dichte Θ – Θ1. Die Dichte der Masse eines Meeresortes M zwischen der Ausgleichungsfläche und dem Meeresgrunde ist Θ + Θ1, und die Dichte des Meereswassers ist Θw. Wenn H die Meereshöhe eines Festlandortes, h die Tiefe der Ausgleichungsfläche und T die Meerestiefe bedeuten, so gelten nach Fig. 1 für die Isostasie der Erdkruste über der Ausgleichungsfläche die Beziehungen
Θ · H + (Θ – Θ1) h = Θ · h = Θw · Ί + (Θ + Θ1) (h – T) und Θ1 : Θ = H : h.
[704] Für die Massenberechnung auf jeder Station hat man die ganze Erdoberfläche in konzentrisch zur Station liegende Ringzonen und diese nochmals durch Halbmesserstrahlen in Abteilungen zerlegt. Hiernach sind die Vertikalkomponenten der Massenanziehungen für 124 Schwerestationen und daraus die Verbesserungen der g-Werte berechnet worden, wobei folgende Werte eingesetzt wurden: h = 117,3, Θ = 2,67 und Θw = 1,027. Näheres s. [3]. Diese Verbesserungen sowie die wegen der Meereshöhen nach + 10-7 3086 H wurden mit umgekehrten Vorzeichen den im Potsdamer System berechneten γ-Werten zugelegt (s. oben). Die so verbesserten g-Werte stimmen mit den gemessenen g-Werten gut überein. Um festzustellen, ob die neue Berechnungsart den älteren Berechnungsarten überlegen ist, wurden die g-Werte der 124 Stationen ferner lediglich nach den in Bd. 8, S. 16, angegebenen ersten beiden Formeln verbessert. Eine topographische Verbesserung wurde also nicht angebracht. Bei einer dritten Berechnung berücksichtigte man nur die Verbesserung wegen der Meereshöhe nach der neueren Formel (s. oben). Die Mittel der absoluten Werte aller Abweichungen gemessene Schwerkraft – berechneter Schwerkraft sind bei den drei Berechnungsarten 0,20 mm, 0,64 mm und 0,29 mm. Die neue Berechnungsart ist also am günstigsten. Außerdem wurden die Beobachtungen nach den geographischen Breiten in sechs Gruppen zusammengefaßt, und danach wurden auf Grund der drei Berechnungsarten auch die Schwereformeln berechnet. Die Berechnung mit Ausgleichung nach der Methode der kleinsten Quadrate ergab für die neue Berechnungsart
γ = 9,78038 (1 + 0,005304 sin2 φ – 0,000007 sin2 2φ).
Daraus bestimmte man die Abplattung, s. Erde, Bd. 3, S. 487, und Clairauts Theorem, Bd. 2, S. 469, zu 1 : 298,4 ± 1,5. Die Abplattungen für die andern beiden Berechnungsarten sind 1 : 280,7 ± 7,2 und 1 : 292,1 ± 1,7. Helmert fand 1 : 298,3 ± 0,7. Auch hiernach zeigte die neue Berechnungsart sich überlegen.
Die Theorie der isostatischen Reduktion behandeln auch Helmert in [4] und Hübner in [5].
Die von Hecker mit Quecksilberbarometern und Siedethermometern ausgeführten Schwerkraftmessungen auf den Ozeanen haben erwiesen, daß die Prattsche Hypothese von der Isostasie der Erdkruste im allgemeinen auch für die Weltmeere gilt, s. Bd. 8, S. 16. Um zu untersuchen, ob die Massen unter dem Binnenmeere ebenfalls isostatisch ausgeglichen sind, unternahm Hecker 1909 Schwerkraftmessungen auf dem Schwarzen Meere. Auf Anregung von Baron Eötvös untersuchte er hierbei auch die Frage, ob die Schwerkraft der Theorie entsprechend von der Fahrtrichtung des Schiffes abhängt und fand, daß es tatsächlich nötig ist, hierfür eine Verbesserung einzuführen. Die Messungen führten Hecker zu dem Ergebnisse, daß die Schwerkraft auf den Tiefen des Schwarzen Meeres annähernd normal ist [6]. Dagegen schließt Wolff aus seinen Untersuchungen der Heckerschen Beobachtungen [7], daß dort keine isostatische Lagerung vorhanden ist. Hecker hat auch seine Beobachtungen auf den Weltmeeren wegen der Fahrtrichtung verbessert. Die neuen Berechnungen ändern aber die Schlußfolgerungen der früheren Veröffentlichungen nicht. Näheres s. [6].
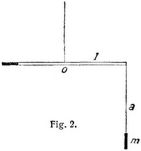
Schon 1896 zeigte Baron Eötvös in [8], daß die Drehwage, s. Bd. 8, S. 821, durch Aenderungen der Schwerkraft eine Drillung (Torsion) erleidet, und daß sie geeignet ist, Aufschluß über die Schwerkraftverhältnisse an der Erdoberfläche und die Krümmung der Geoidfläche zu geben. Eötvös hat zahlreiche Messungen vorgenommen und in [9] über seine Erfolge berichtet. Bei einer einfachen Form seiner Drehwage sind Platingewichte in einen wagerecht schwebenden, etwa 40 cm langen, zylindrischen Hohlstab an beiden Enden eingeschoben. Bei einer andern Form, dem Schwerevariometer, Fig. 2, ist das eine Gewicht unterhalb des Stabes aufgehängt. Die Drehwage wird von einer Säule getragen, die um die Achse eines geteilten Horizontalkreises verstellt werden kann. Trotz des geringen Abstandes der Gewichte sind die Größe und Richtung der Schwerkraft, die auf beide wirken, nicht ganz gleich, so daß die Wage sich etwas dreht, x, y, z seien die Koordinaten eines Massenteilchens eines der beiden Gewichte in einem rechtwinkligen Koordinatensysteme im Räume, dessen Nullpunkt 0 im Schwerpunkte des Gehänges liegt, dessen x-Achse nach Norden und dessen z-Achse senkrecht abwärts gerichtet sind. Bedeuten W das Potential der Schwerkraft, K das Trägheitsmoment des Gehänges, D die Torsionskonstante des Drahtes und α das Azimut der Stabachse mit der x-Achse, so ist der Winkel D, um den die Schwerkraft die Wage der ersten Form aus der drillungsfreien Lage dreht,
Für die Drehwage der zweiten Form treten rechts noch die beiden Glieder
hinzu. Hierin sind m die tiefer gehängte Masse, α ihr senkrechter Abstand von der Stabachse und l die Länge ihres Drehungsarmes. Sind die Unveränderlichen K, D, m, a und l der Instrumente bekannt, so hat man für die Drehwage erster Form die drei Unbekannten
D, (∂2W : ∂y2 – ∂2W : ∂x2) und ∂2W : ∂ x ∂ y
und für die Drehwage zweiter Form außerdem noch die beiden Unbekannten
∂2W : ∂ x ∂ z und ∂2W : ∂ y∂ z.
Die Werte m, a und l können unmittelbar gemessen werden. K und D sind durch geeignete Beobachtungen zu ermitteln, s. Bd. 8, S. 821. Zur Bestimmung der Unbekannten genügen im ersten Falle drei, im zweiten Falle fünf Ablesungen an den Instrumenten bei verschiedenen, nach dem Horizontalkreise gleichmäßig verteilten Azimuten α, von denen das Anfangsazimut α = 0° nach einem Kompasse eingestellt wird.
[705] Durch die Bestimmung der beiden zuletzt genannten Unbekannten erhält man ohne weiteres die Aenderungsgeschwindigkeit von g nach Norden und Osten
∂2W : ∂ x ∂ z = ∂ g : ∂ x und ∂2W : ∂ y ∂ z = ∂ g : ∂ y,
ebenso das Azimut, in dem sie am größten ist, nach
tgμ1 = (∂2 W : ∂ y ∂ z) : (∂2W : ∂ x ∂ y).
Ihr größter Wert ist ∂ s:
Die Aenderung der Lotrichtung mit der Höhenänderung, wenn diese gering ist, wird angegeben durch l : r = (∂ g : ∂ s) : g, worin g anderweit bestimmt sein muß. Das Umgekehrte hiervon ist der Krümmungshalbmesser der Schwerkraftlinie. In einem beliebig langen Zuge und damit auch in einem ganzen Netze von Schwerestationen kann man den Verlauf der Schwerkraft schrittweise bestimmen durch Berechnen der Schwereänderungen zwischen je zwei benachbarten Punkten. Ferner erhält man den Unterschied der umgekehrten Werte der Hauptkrümmungshalbmesser g1 und g2 einer Niveaufläche und die Richtung der Hauptkrümmung nach
Eötvös gibt auch Verfahren an, durch welche die Beobachtungen von den Störungen der zunächst gelegenen Massen befreit werden, und berücksichtigt dabei topographische Werte und kartographische Wirkungen. Um die Beobachtungszeit einzuschränken, benutzt Eötvös das Doppelschwerevariometer, in dem zwei einfache Variometer derart vereinigt sind, daß die Gewichte einander gegenüberhängen. Hecker hat ein solches Instrument des preußischen Geodätischen Instituts mit Vorrichtungen versehen, die sein vollständig selbsttätiges Arbeiten ermöglichen [10]. Brillouin untersuchte mit einer Drehwage die Krümmungsverhältnisse des Geoids im Simplontunnel [11]. Näheres s. [8]–[13] und [4],
Literatur: [1] Veröffentl. d. Kgl. preuß. Geod. Inst, Berlin 1906; Kühnen und Furtwängler, Bestimmung der absoluten Schwerkraft zu Potsdam. – [2] Verhandl. d. XVI. allg. Kons.d. intern. Erdm. 1909 in London, III. Teil, Berlin 1911; Borras, Bericht über die relativen Messungen der Schwerkraft mit Pendelapparaten in der Zeit von 1808 bis 1909 und über ihre Darstellung im Potsdamer Schweresystem. – [3] Hayford u. Bowie, The effect of topographie and isostatic compensation upon the itensity of gravity, Coast and Geodetic Survey, Washington 1912; Bowie, Effect u.s.w. (Second paper), desgl., das. 1912. – [4] Enzyklop. d. math. Wissensch. VI, 1 B., 2, 1910; Helmert, Die Schwerkraft und die Massenverteilung der Erde. – [5] Beitr. z. Geophys. XII, 4, 1913; Hübner, Beitrag zur Theorie der isostatischen Reduktion der Schwerebeschleunigung. – [6] Zentralbureau d. intern. Erdm.; Hecker, Bestimmung der Schwerkraft auf dem Schwarzen Meere und dessen Küsten sowie neue Ausgleichung der Schwerkraftmessungen auf dem Atlantischen, Indischen und Großen Ozean, Berlin 1910. – [7] Wolff, Die Schwerkraft auf dem Meere und die Hypothese von Pratt, 1913. – [8] Ann. d. Phys.u. Chem., Bd. 59, 1896, S. 354; Eötvös, Untersuchungen über Gravitation und Erdmagnetismus. – [9] Verhandl. d. XV. allgem. Kons.d. intern. Erdm. 1906 in Budapest, I. Teil, S. 337, d. XVI. 1909 in London, I. Teil, S. 319; Eötvös, Bericht über die geodätischen Arbeiten in Ungarn. – [10] Zeitschr. f. Instr. 1910, S. 6; Hecker, Die Eötvössche Drehwage des Kgl. Geodät. Institutes in Potsdam. – [11] Zeitschr. f. Verm. 1909, S. 543; Messerschmidt, Eine neue Methode zur Bestimmung der Krümmungsverhältnisse des Geoids. – [12] Ebend. 1913, S. 474; Eggert, Theorie und Anwendung der Drehwage von Eötvös. – [13] Messerschmidt, Die Schwerebestimmungen der Erdoberfläche, Braunschweig 1908.
Hillmer.
http://www.zeno.org/Lueger-1904.